Décomposition en idempotents d'une fonction non bijective
Olympiades mathématiques, énigmes et défis
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 19 Déc 2010, 14:27
Hello !
E est un ensemble
fini et non vide et
une application. On suppose qu'il existe une partie X de E telle que
est injective non surjective.
1) Montrer qu'il existe un nombre fini d'applications
)
telles que
pour tout i et pour tout x dans X,
=(p_{1}o...op_{n})(x))
.
Indication donnée avec l'énoncé : On pourra discuter selon si
\subset X)
ou non.
2) Montrer plus généralement que toute application non bijective se décompose en produit d'applications idempotentes.
Amusez-vous bien !
:happy3:
-
windows7
- Membre Rationnel
- Messages: 548
- Enregistré le: 18 Juin 2010, 11:00
-
par windows7 » 19 Déc 2010, 15:14
permutons permutons :D
"montrez qu'il ya un a nombre fini .. " ca me parait etrange de poser l question comme ca vu que de toute facon il n'y a qu'un nombre fini d'application de E dans E
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 19 Déc 2010, 15:42
Salut,
ça m'avait un peu dérangé aussi à première lecture mais après tout le fait d'avoir un ensemble fini n'empêche pas de considérer une infinité d'éléments, il suffit d'autoriser à ce qu'ils ne soient pas distincts !
Autrement dit, on peut toujours faire des produits infinis même sur un ensemble fini... Ici, l'important est que l'application se décompose en produit fini.
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 20 Déc 2010, 12:08
Salut,
Il me semble qu'il y a un problème dans l'énoncé : si f est bijective et
\geq 2)
alors en prenant pour
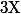
un singleton l'application
est évidement injective et non surjective alors que le résulat est clairement faux...
Je vais donc plutôt regarder le 2)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 20 Déc 2010, 15:35
Pas d'idées?
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 20 Déc 2010, 17:01
Salut,
Soit
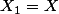
et
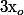
un élément fixé de
.
Si
\not\subset X_1)
soit
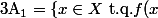\not\in X\})
,
\ {\rm si } x\in A_1\cr \ \ x\ \ \ {\rm sinon }}\right.)
(idempotente) et
Si
\not\subset X_2)
, etc.
Vu qu'on enlève au moins un élément à chaque fois, le processus s'arrète et on tombe sur un
tel que
\subset X_n)
, c'est à dire
=X_n)
(le caractère "injectif et non surjectif" se conserve bien sûr lors des restrictions).
On peut évidement enlever de
les
tels que
=x)
Si
, on considère un cycle
,f^2(a),...,f^d(a)=a)
de
et les applications idempotentes suivantes :
,
\cr x\ {\rm sinon }}\right.)
,
\ {\rm si } x=f^{d-2}(a)\cr \ \ \ x\ \ \ \ \ \ {\rm sinon }}\right.)
. . . ,
\ {\rm si } x=f(a)\cr\ \ \ x\ \ \ \ {\rm sinon }}\right.)
,
\ {\rm si } x=x_o\cr x\ \ \ {\rm sinon }}\right.)
Si on a pas épuisé
on recommence avec un autre cycle.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
par Nightmare » 20 Déc 2010, 17:42
Niquel comme d'hab. Ensemble fini + bon dessin => solution.
:happy3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 11 invités
