Un début de transcendance pour e

par **Nightmare** » 13 Déc 2010, 21:59

Hello !

Aujourd'hui, un bouquin m'a encore appris que e était transcendant. Si je suis toujours incapable d'en restituer une preuve complète, je me suis rappelé aujourd'hui d'une de mes khôlles de sup' qui elle est restée en mémoire. Bizarre d'ailleurs que je ne l'ai pas déjà postée :

Sauriez-vous montrer que e n'est pas racine d'un polynôme rationnel (non nul) du second degré? (5-6 lignes :lol3: )

Précision :

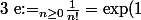A vos stylos.

:happy3:

par **Zweig** » 13 Déc 2010, 22:25

On établit l'expression en fraction continue d'exp(x) ; on en déduit alors celle de e. Or on montre qu'elle n'est pas périodique donc e ne peut être racine d'une équation polynominale à coefficiens rationnels.

CQFD.

:we:

:jesors:

par **Ben314** » 13 Déc 2010, 22:42

Zweig a écrit:On établit l'expression en fraction continue d'exp(x) ; on en déduit alors celle de e. Or on montre qu'elle n'est pas périodique donc e ne peut être racine d'une équation polynominale à coefficiens rationnels.

CQFD.

:jesors:

NON : la non périodicité du développement en fraction continues montre seulement qu'un nombre n'est pas solution d'un polynôme de degrés 2 à coeff rationnels !

par **Zweig** » 13 Déc 2010, 22:45

oui, j'ai omis de la préciser ; non mais de toute manière mon message n'était qu'une "boutade", même si mathématiquement c'est vrai

par **Nightmare** » 13 Déc 2010, 22:46

Ben314 a écrit:NON : la non périodicité du développement en fraction continues montre seulement qu'un nombre n'est pas solution d'un polynôme de degrés 2 à coeff rationnels !

Ah ben en même temps c'est ce qu'on veut !

par **Nightmare** » 13 Déc 2010, 22:55

Bon, pour ceux qui cherchent où partir, la preuve que j'ai est analytique, pas étonnant :lol3:

par **Nightmare** » 15 Déc 2010, 16:24

Salut à tous !

pour ceux que ça intéresse, le principe de la preuve est d'appliquer un théorème de Taylor à

où a et b sont bien choisis.

par **Zweig** » 15 Déc 2010, 18:56

Sans cette indication, comment on était censé trouver ce polynôme ?

par **Nightmare** » 15 Déc 2010, 19:01

De quel polynôme parles-tu ?

par **Zweig** » 15 Déc 2010, 19:09

Oulà, désolé, j'avais pa sfait gaffe à cette boulette. Je voulais bien sûr parler de ta fonction.

par **Nightmare** » 15 Déc 2010, 19:14

Ah, dans ce cas :

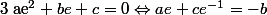
:happy3:

par **ppcrepin** » 30 Déc 2010, 11:57

tu appliques une formule de Taylor en 1 à la fonction que tu as défini plus haut c'est ça?
et on est censé trouver une absurdité .

par **Nightmare** » 30 Déc 2010, 12:19

On peut procéder un peu comme la preuve de son irrationalité.

Avec f(x)=aexp(x)+cexp(-x) , Taylor-Lagrange à l'ordre n fournit :

pour un certain tn dans

Et, par hypothèse, f(1)=-b donc est entier. Multiplier ce qu'on a obtenu au dessus par n! et voir ce qu'il se passe.

par **ppcrepin** » 30 Déc 2010, 13:03

d'accord merci !

par **benekire2** » 30 Déc 2010, 13:12

Salut,

Sinon, existe-il une autre preuve ?

par **ffpower** » 30 Déc 2010, 16:38

Ben ya la preuve de la transcendence, qui en particulier implique ça :we:

par **benekire2** » 30 Déc 2010, 16:47

ffpower a écrit:Ben ya la preuve de la transcendence, qui en particulier implique ça :we:

Tu aime écraser une fourmi avec un char d'assaut :ptdr:

par **ffpower** » 30 Déc 2010, 16:59

Oui, c'est mon coté sadique :lol3:

par **benekire2** » 30 Déc 2010, 17:08

ffpower a écrit:Oui, c'est mon coté sadique :lol3:

Je le savais !! :zen:

Plus sérieusement , c'est la même preuve que dans le Oraux X-ENS, mais il doit y en avoir d'autres :id:

par **Nightmare** » 30 Déc 2010, 17:18

Je crois qu'effectivement ça a été posé à L'X où aux ENS (vu le caractère algébrique de la question, j'aurais dit aux ENS)

Un début de transcendance pour e

un début de transcendance pour e

Qui est en ligne