Darboux
Olympiades mathématiques, énigmes et défis
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 12 Avr 2019, 17:51
par MMu » 12 Avr 2019, 17:51
Soient les fonctions
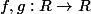
(réels), telles que

croisante et

continue.
Montrer que si
-g(-3)>f(3)-g(3))
alors
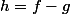
a la propriété des
valeurs intermédiaires : pour tout

entre
,h(3))
il existe
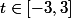
tel que
=y)

-
ffback
- Membre Relatif
- Messages: 101
- Enregistré le: 08 Mar 2016, 19:54
-
 par ffback » 16 Avr 2019, 14:49
par ffback » 16 Avr 2019, 14:49
Pourquoi sur [-3,3]? étrange comme choix d'intervalle. Mais bref:
Soit
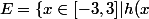\geq y\})
. Il est non vide (contient -3), majoré (par 3), notons

. Alors:
-pour tout

dans

,

et
\geq y)
donc
=f(x)-g(x)\leq f(t)-g(x))
donc en faisant tendre

vers

,
-g(t)=h(t))
.
-pour tout

majorant strict de

,
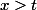
et
<y)
donc
=f(x)-g(x)>f(t)-g(x))
donc en faisant tendre

vers

,
-g(t)=h(t))
.
Donc
=y)
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités

