Critère de permutabilité

[Arbre]

énoncé 6 : critère de permutabilité
Soit une fonction de dans lui même, avec premier impair.
A-t-on permutation ssi ?

[Ben314]

Bis et répéta : on l'a déjà fait récemment ici :
enigmes/critere-hermite-t180441.html
Pour tout est l'indicatrice de donc est une permutation ssi pour tout .
Sauf qu'en développant, on trouve que .

[Arbre]

Non, ce n'est pas du tout le même résultat par contre, ma réponse reste la même :
https://www.maths-forum.com/enigmes/facile-simple-sont-pas-confondus-t181279-20.html#p1203243

édit : Non pour ton résultat vous avez besoin de l'hypothèse plus forte concernant les racines de , dans ton résultat il faut une seule racine dans le mien il en faut au moins une et moins de p.
Donc OUI ce n'est pas le même résultat.

[Ben314]

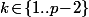
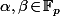
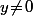
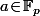
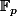
Si pour alors il existe tels que, pour tout (c.f. post précédent) donc pour tout ce qui, vu que est la somme des indicatrices des pour , signifie que toute les valeurs non nulles de apparaissent le même nombre de fois (modulo ) parmi les différents .
Les seuls cas possibles sont donc :
- Elle apparaissent toutes 0 fois, donc est constante égale à zéro.
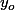
- Elle apparaissent toutes 0 fois, sauf une qui apparait fois donc est constante égale à .
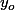
- Elle apparaissent toutes 1 fois, donc 0 apparait lui aussi une fois et est une permutation.

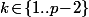
Bilan : pour si et seulement si est constante ou bien est une permutation.

Et je répète (pour la 3em fois...) que cette constatation, Doraki l'avais déjà faite dans l'autre Thread.