Salut,
Je viens finir la correction du bouquin ici, au cas où quelqu'un retombe sur le même problème (c'est issu d'un exercice du livre "algèbre concrète" de Maurice Mignotte). Je suis désolé si je répète ce qui a été dit, j'ai pas le courage de tout relire

. On commence par poser comme
lemme (comme l'a constaté Doraki) que pour
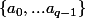
q éléments de
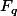
on a les équivalences suivantes:
(i)
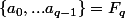
(ii)
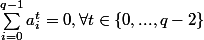
tel que p ne divise pas t et
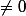
pour t=q-1
(iii)
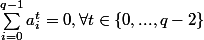
et
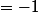
pour t =q-1
Pour le montrer on pose justement
=1-(x-a_i)^{q-1}=1-\sum_{j=0}^{q-1}a_i^{q-1-j}x^j)
(la deuxième inégalité est justifiée par le premier post). Mais c'est aussi et surtout l'indicatrice de

. Ainsi avec
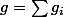
on a :
(*) les

sont distincts si et seulement si g est constance égale à 1. L’intérêt de l'écriture sous forme de somme est qu'on peut écrire g comme un polynôme en X.
=\sum_{i=0}^{q-1}1-\sum_{i=0}^{q-1}\sum_{j=0}^{q-1}a_i^{q-1-j}X^j)
X^j)
en supposant (i) c'est un polynôme à coefficients dans un corps et qui coïncide en q points avec 1. C'est donc g=1 et on en déduit le point (iii) la réciproque se fait de la même façon sachant que (*) est une équivalence.
On a en plus trivialement (iii) implique (ii) et sachant (ii) en écrivant
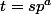
tel que s ne divise pas p, on obtient (iii).
On peut ensuite s'attaquer au critère d'Hermite ; On prend
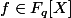
une permutation
La première condition du critère est facile. Pour la deuxième condition j'ai pas compris ce que l'auteur a fait donc j'ai essayé de faire à ma sauce... Mea culpa si c'est pas correct ou inutilement compliqué

.
On remarque déjà que puisque
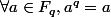
, f et [f] (f modulo
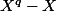
ont la même image quand on leur fait manger un élément de
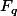
. Donc avec t<q-1 et
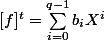
on a
=0=\sum b_i \sum_{a\in \mathsbb{F_q}} a^i=b_{q-1})
donc on on a bien la deuxième condition.
Avec des arguments du même genre, la réciproque est pas compliquée.
Pour ce qui est des implications du critère, y en a une que l'auteur donne que je trouve méga super cool :
Corollaire:Soit
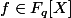
de degré d qui divise q-1 alors f n'est pas une permutation.
La démonstration tient en une ligne :
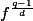
est de degré q-1 donc la deuxième condition d'Hermite n'a pas lieu.
ça redémontre que par exemple le carré n'est jamais surjectif dans les corps finis mais par exemple on sait qu'un polynôme de degré 5 ne sera jamais une permutation dans
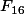
entre autre.
Voilà voilà, j'espère avoir pu éclairé quelqu'un!
avec
premier et
et
.
:
est une permutation de
si et seulement si :
admet exactement une racine dans
.
t.q.
, si
est le reste de la division de
par
, on a
.

 . On commence par poser comme
. On commence par poser comme 