Au revoir.
Coup de Boole
16 messages
- Page 1 sur 1
Re: Coup de Boole
Pour moi, on déduit que c'est vrai grâce au fait que m!(n-m+u)! / u! est pair dés que n>=m et u>=0 (et n>=3).
Re: Coup de Boole
J'écris  = \sum_{k=1}^{2^n} a_k x_1 ^{k(1)}...x_n^{k(n)}) où a_k = 0 ou 1 et k(i) désigne le i eme chiffre dans l'écriture binaire de k (on vérifie bien que cette écriture est possible, c'est chiant mais facile).
où a_k = 0 ou 1 et k(i) désigne le i eme chiffre dans l'écriture binaire de k (on vérifie bien que cette écriture est possible, c'est chiant mais facile).
Notre somme devient}^{k(1)}...x_{\phi(n)}^{k(n)}) avec
avec 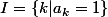
Et maintenant je suis en train de douter de l'intitulé de ta question. Qu'est ce que le "mod 2" vient faire ici sachant qu'on parle de booléen ? Si tu considères f comme simplement une fonction de {0,1}^n dans {0,1} alors ok, la suite de ma démonstration consiste à compter le nombre de permutations phi telles que, à k donné,}^{k(1)}...x_{\phi(n)}^{k(n)} = 1) .
.
Ce genre de permutation, c'est juste les permutations qui envoient =1\}) vers
vers 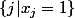 , 2 ensembles qui sont fixés par la donnée de
, 2 ensembles qui sont fixés par la donnée de ) et f. On peut finalement compter ces permutations et montrer que ce nombre est pair (les nombres de mon post précédent). Du coup on fait une somme de trucs pairs, ce qui donne une somme finale paire.
et f. On peut finalement compter ces permutations et montrer que ce nombre est pair (les nombres de mon post précédent). Du coup on fait une somme de trucs pairs, ce qui donne une somme finale paire.
Si maintenant on s'intéresse à la valeur booléenne de notre somme, pour qu'elle vaille 1 il faut qu'au moins un élément vaille 1, et donc qu'il existe une permutation phi qui envoie =1\}) vers
vers 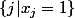 et donc que
et donc que 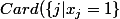 \geq Card(\{i | k(i) =1\})) .
.
La somme vaut donc 1 si =1\})) \leq Card(\{j | x_j =1\})) , 0 sinon.
, 0 sinon.
Notre somme devient
Et maintenant je suis en train de douter de l'intitulé de ta question. Qu'est ce que le "mod 2" vient faire ici sachant qu'on parle de booléen ? Si tu considères f comme simplement une fonction de {0,1}^n dans {0,1} alors ok, la suite de ma démonstration consiste à compter le nombre de permutations phi telles que, à k donné,
Ce genre de permutation, c'est juste les permutations qui envoient
Si maintenant on s'intéresse à la valeur booléenne de notre somme, pour qu'elle vaille 1 il faut qu'au moins un élément vaille 1, et donc qu'il existe une permutation phi qui envoie
La somme vaut donc 1 si
Re: Coup de Boole
Nul part tu n'utilises le fait que 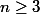 , or si on prend f(0,1)=0 et f(1,0)=1 on voit bien qu'ici cela ne marche pas.
, or si on prend f(0,1)=0 et f(1,0)=1 on voit bien qu'ici cela ne marche pas.
Re: Coup de Boole
Pour ce qui est de ton résultat précédent où tu mentionnes bien le fait n>2.
1/ Comment montres-tu que cela, correspond à ce que tu comptes ?
2/ Comment montres-tu que ce nombre est bien pair ?
1/ Comment montres-tu que cela, correspond à ce que tu comptes ?
2/ Comment montres-tu que ce nombre est bien pair ?
Re: Coup de Boole
Tu n'as pas la même formule que Matt, lui divise par une factorielle, mais les questions que j'ai posé à Matt, tu n'y réponds pas non plus.
Re: Coup de Boole
c'est surement généralisable, mais cela ne répond pas à mes questions, ou alors il faudrait me dire comment.
Re: Coup de Boole
Si on note m le nombre de 1 dans k, p le nombre de 1 dans x :
On a p choix pour le premier 1 dans k, p-1 pour le deuxième etc ce qui donne p!/(p-m)!
Pour les n-p restants termes à déterminer, on a n-m choix puis n-m-1 puis ... puis 1.
Le résultat final est donc p!(n-m)!/(p-m)! qui est tout le temps pair pour n>=3.
On a p choix pour le premier 1 dans k, p-1 pour le deuxième etc ce qui donne p!/(p-m)!
Pour les n-p restants termes à déterminer, on a n-m choix puis n-m-1 puis ... puis 1.
Le résultat final est donc p!(n-m)!/(p-m)! qui est tout le temps pair pour n>=3.
Re: Coup de Boole
Si p!/(p-m)! est impair alors p = 1 ou p=0 ou m=1.
Dans tous ces cas là, (n-m)! est pair (m<=p).
C'est usant de vouloir tant de justifications, c'est clairement évident par rapport au niveau du problème.
Dans tous ces cas là, (n-m)! est pair (m<=p).
C'est usant de vouloir tant de justifications, c'est clairement évident par rapport au niveau du problème.
16 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 5 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

