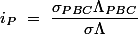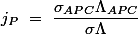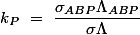salut , un truc sympa à propos :
Relations entre des coordonnées barycentriques normalisées et des aires algébriques
On se donne l'application
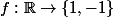
définie par
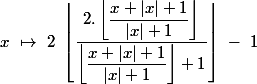
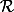
est un repère orthonormé du plan affine muni d'une structure d'espace vectoriel et de la distance euclidienne
\)
une base affine de ce plan
Pour tout point
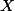
du plan , on propose les notations
\)
sont les coordonnées cartésiennes du point
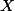
sur
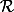
\)
sont les coordonnées barycentriques normalisées du point
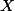
sur
\)
On pose
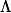
est l'aire (géométrique) du triangle
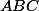
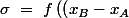\ \left(y_C-y_A\right)\ -\ \left(x_C-x_A\right)\ \left(y_B-y_A\right)\right))
Soit
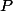
un point quelconque du plan
on pose
\ \left(y_C-y_P\right)\ -\ \left(x_C-x_P\right)\ \left(y_B-y_P\right)\right))
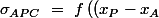\ \left(y_C-y_A\right)\ -\ \left(x_C-x_A\right)\ \left(y_P-y_A\right)\right))
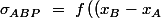\ \left(y_P-y_A\right)\ -\ \left(x_P-x_A\right)\ \left(y_B-y_A\right)\right))
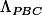
est l'aire (géométrique) du triangle
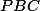
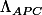
est l'aire (géométrique) du triangle
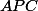
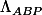
est l'aire (géométrique) du triangle
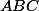
Alors les produits

sont des aires algébriques de triangles
et on obtient les trois relations