Cosinus
Olympiades mathématiques, énigmes et défis
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 14 Juil 2006, 19:03
par nekros » 14 Juil 2006, 19:03
Soit

définie par
 = cos(a_1 + x) + \frac{1}{2}cos(a_2 + x) + \frac{1}{4} cos(a_3 + x) + ... + \frac{1}{2^{n-1}} cos(a_n + x)})
, où les
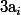
sont des réels fixés et

une variable de
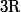
Si
 = f(x_2) = 0)
, prouvé que
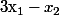
est un multiple de
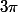
.
Bonne chance.
Thomas G :zen:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 14 Juil 2006, 20:30
par aviateurpilot » 14 Juil 2006, 20:30
si je me souviens
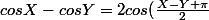cos(\frac{X+Y-\pi}{2}))
et
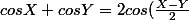cos(\frac{X+Y}{2}))
donc
-f(x_2)=2cos(\frac{x_1-x_2+\pi}{2})f(\frac{x_1+x_2-\pi}{2}))
si
-f(x_2)=0)
alors
=0)
ou
=0)
donc
=0)
ou

(1)
en plus
+f(x_2)=2cos(\frac{x-1-x_2}{2})f(\frac{x-1+x_2}{2}))
si
+f(x_2)=0)
alors
=0)
ou
=0)
donc
=0)
ou

(2)
doncsi
=f(x_2)=0)
alors

sinon il faut que
=f(\frac{x-1+x_2-\pi}{2})=0)
on fait la meme chose avec

et
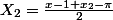
si on repete la meme chose avec

et

on va trouver un
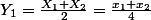
et

....
....etc
....(n fois)
.....
....
on trouve que
=f(quelquechose)=0)
quelque soit n d N*
si on prend n>a avec
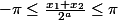
on va trouve que f a une infinité de racine entre 0 et

(car f est de periode

)
ce qui est absurde
donc la seul possibilité est

-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 21 Juil 2006, 15:12
par aviateurpilot » 21 Juil 2006, 15:12
qui as une autre methode?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités