Cos ...

[mathlegend]

bonjour
soit des réels tel que =
prouver que
>=

[mathlegend]

aucune personne

[vincentroumezy]

Demande à Olympus.

[windows7]

|cos(a)|+..|cos(e)| > |cos(a)+..cos(e)|
f(a,b,c,d,e)=cos(a)+..cos(e)
contrainte : a+b+c+d+e=0
df/da=sin(a)
.
.
df/de=sin(e)

il existe donc k reel tq
sin(a)=k
.
.
sin(e)=k

=> a=..=e [2pi]
alors b=2pib'+a,...e=2pie'+a

la contrainte donne donc 5a+2pi(b'+..e')=0
donc 5a=0[2pi]=> a=2npi/5

reste a regarder h(n)=5*cos(2pi n/5 )

reste a traité les autres cas, bref c'est dla merde ce truc

[Zweig]

Un indice ? Je sèche ...

[Ben314]

Salut,
Ca se fait par une simple étude de fonction :

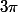
Quitte à ajouter/retrancher des multiples de aux variables, on peut supposer que ce qui fait que les cosinus sont tous positifs (donc plus de valeur absolue) mais que l'hypothèse se réécrit .

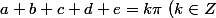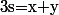
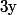
Or, si, on étudie pour de somme fixée la quantité , c'est à dire si on étudie (dérivée) la fonction pour , on voit que cette fonction est minimale sur un des deux "bord" de l'intervalle, c'est à dire lorsque ou vaut .

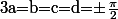
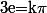
On en déduit que la somme est minimale lorsque et donc lorsque c'est à dire .
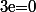
Dans ce cas,