Bonjour à tous,
je suis confronté à un petit problème anodin que je vous présente via une analogie :)
Bon amusement.
Un comptable souhaite imprimer la liste des opérations réalisées depuis le début de l'année.
Pour cela il dispose d'une imprimante spéciale capable d'imprimer sur des feuilles découpées sur-mesure (pour simplifier, on exprimera la taille d'une feuille en nombre de ligne).
Cependant, le comptable a certaines contraintes:
1. L'imprimante ne peut pas changer la taille des feuilles au cours de l'impressions (les feuilles ont toutes le même nombres de lignes).
2. Le nombre de lignes que contient une feuille (sa taille) doit être un entier.
3. Il existe un intervalle de lignes de taille et de position arbitraire qui doivent impérativement être imprimé sur la même feuille
La question est "combien de lignes par page le comptable doit-il choisir pour avoir les feuilles les plus petites possibles?"
Par exemple, l'intervalle a imprimer sur la même page concerne les ligne 3 à 6 (4 lignes donc). Si je choisis une taille de feuille de 4 alors les ligne 1,2,3 et 4 seront imprimées sur une page et la ligne 5,6,7 et 8 sur une autre. Les lignes 3,4,5 et 6 sont donc imprimées sur 2 pages différentes et la solution n'est pas correcte.
Si j'imprime 20 lignes par feuille, effectivement les lignes 3 à 6 sont sur la même feuille mais il existe des tailles de feuilles plus petites qui conviennent or on veut la taille minimale :)
Un comptable dur de la feuille
6 messages
- Page 1 sur 1
Bonjour, je dirais que si on doit inclure les n lignes numérotées de i à i+n-1 alors le nombre minimal de lignes par feuille est le plus petit diviseur de i+n-1 qui soit supérieur à n.
Par exemple si on doit inclure les lignes de 3 à 6, ça correspond à i = 3, n = 4 et i+n-1 = 6. Le plus petit diviseur de 6 supérieur à 4 est 6 lui-même, donc on écrit au mieux 6 lignes par feuille. En revanche si on doit inclure les lignes de 5 à 8, i = 5, n = 4 et i+n-1 = 8 donc on peut se contenter de 4 lignes par feuille.
Sauf erreurs.
Edit : hum en fait ma solution marche pas, si on doit inclure les lignes 10 et 11, ma solution donne 11 lignes par feuille alors qu'on peut s'en contenter de 3.
Par exemple si on doit inclure les lignes de 3 à 6, ça correspond à i = 3, n = 4 et i+n-1 = 6. Le plus petit diviseur de 6 supérieur à 4 est 6 lui-même, donc on écrit au mieux 6 lignes par feuille. En revanche si on doit inclure les lignes de 5 à 8, i = 5, n = 4 et i+n-1 = 8 donc on peut se contenter de 4 lignes par feuille.
Sauf erreurs.
Edit : hum en fait ma solution marche pas, si on doit inclure les lignes 10 et 11, ma solution donne 11 lignes par feuille alors qu'on peut s'en contenter de 3.
Bonsoir,
J'ai l'impression que c'est plus vicieux que ça.
En reprenant les notations de Skullkid : on veut que les lignes à
à  soit sur une même page (
soit sur une même page ( et
et  connus)
connus)
Si L est la longueur d'une page, alors la k-ième page va contenir les lignesL+1) à
à  .
.
Donc on aimerais qu'il existe t.q.
t.q. L+1\leq i) et
et 
Si on fait la division euclidienne de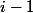 par
par  :
: 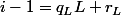 avec
avec  , le mieux qu'on ait est
, le mieux qu'on ait est  ce qui donne pour la première équation
ce qui donne pour la première équation 
Mais je pense pas que le min des L soit forcément dans la catégorie " "...
"...
J'ai l'impression que c'est plus vicieux que ça.
En reprenant les notations de Skullkid : on veut que les lignes
Si L est la longueur d'une page, alors la k-ième page va contenir les lignes
Donc on aimerais qu'il existe
Si on fait la division euclidienne de
Mais je pense pas que le min des L soit forcément dans la catégorie "
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:
Salut Ben314, en mauvais élève j'avais juste noté le reste "r", sans faire apparaître explicitement la dépendance en L, du coup j'en avais brillamment conclu que le plus petit L satisfaisant cette inégalité est évidemment n+r :mur:
Histoire de réécrire les choses de façon pédante, on cherche le minimum de l'ensemble des solutions L de l'inéquation
Le problème à l'air très difficile à traiter. J'ai essayé de chercher les situations où la taille des pages était les plus grosses par rapport au nombre de lignes. En voici quelque unes:











Edit: On dirait qu'il y a une relation entre les nombres premiers et les i trouvés.
68468399 et 107881199 sont premiers! :marteau:
Edit: On dirait qu'il y a une relation entre les nombres premiers et les i trouvés.
68468399 et 107881199 sont premiers! :marteau:
Je ne pense pas qu'il y ait réellement un lien avec les nombres premiers.
Et ton "i", j'ai l'impression que c'est plutôt le i-1 de skullskid mais ça risque de vouloir dire que les lignes tu a commencé à les numéroter à 0 (et ton "L" c'est son "n" et ton "S", c'est son "L"...).
Donc, avec tes notations le fait que, par exemple L=3 et i=68 468 399 donne un S=27 signifie très précisément que :
Ton i, si on note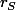 le reste de sa division par S, alors pour tout S entre 3 et 26, on a
le reste de sa division par S, alors pour tout S entre 3 et 26, on a  (et par contre
(et par contre  ).
).
Cela implique en particulier que, pour S entre 3 et 26, c'est à dire que ton i ne se divise par aucun entier compris entre 3 et 26.
c'est à dire que ton i ne se divise par aucun entier compris entre 3 et 26.
A mon avis, cela peut suffire à expliquer qu'il y a une probabilité non négligeable que ton i soit premier (en tout cas beaucoup beaucoup plus grande que si tu prenait un nombre de cette taille au hasard)
Et ton "i", j'ai l'impression que c'est plutôt le i-1 de skullskid mais ça risque de vouloir dire que les lignes tu a commencé à les numéroter à 0 (et ton "L" c'est son "n" et ton "S", c'est son "L"...).
Donc, avec tes notations le fait que, par exemple L=3 et i=68 468 399 donne un S=27 signifie très précisément que :
Ton i, si on note
Cela implique en particulier que, pour S entre 3 et 26,
A mon avis, cela peut suffire à expliquer qu'il y a une probabilité non négligeable que ton i soit premier (en tout cas beaucoup beaucoup plus grande que si tu prenait un nombre de cette taille au hasard)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
