Composition interne

par **aviateurpilot** » 04 Juin 2006, 00:45

cardE=n

combien de lois de composition interne exitent dans une ensembe E ?

" je l'ai trouvé dans mon livre scolaire de math cacher entre des exo faciles "

par **yos** » 04 Juin 2006, 10:38

car ce sont les applications de E² dans E.

par **aviateurpilot** » 04 Juin 2006, 10:43

oui. c ca
moi . puisque je ne retien pas mon cours tres bien
j'utilise tjrs mon imagination pour resoudre ces exo
car j ai oublié que le nombre d'applications de E vers F:
cardF ^ cardE

par **Zebulon** » 04 Juin 2006, 10:48

aviateurpilot a écrit:oui. c ca
moi . puisque je ne retien pas mon cours tres bien
j'utilise tjrs mon imagination pour resoudre ces exo
car j ai oublié que le nombre d'applications de E vers F:
cardF ^ cardE

Bonjour,
comment faites-vous alors? Vous revenez au dénombrement des applications de E dans F?

par **aviateurpilot** » 04 Juin 2006, 10:58

on suppose qu'on a cardE boites
et on doit mettre un element de F dans chaque boite
(la boite a contien B <=> l'image de a c'est B)
puisqu'on a cardF boite et on doit mettre mettre un element de F dans chaque boite et on a le droit de répéter

dans le 1er boite il y a cardF choix
dans le 2eme boite il y a cardF choix
dans le 3eme boite il y a cardF choix
..................
dans le (cardE)eme boite il y a cardF choix
donc le nombre d'application c'est cardF^cardE

par **yos** » 04 Juin 2006, 10:59

Alors fais marcher ton imagination : Combien de ces lois internes sur E sont commutatives?

par **aviateurpilot** » 04 Juin 2006, 11:03

dans ce cas on remplace les 2 boite qui correspand a a*b et b*a par une seul boite

par **aviateurpilot** » 04 Juin 2006, 11:05

n^[(n-1)n/2]
avec n=cardE

par **yos** » 04 Juin 2006, 11:13

Plutôt

non?

par **aviateurpilot** » 04 Juin 2006, 11:26

mais n(n+1)/2
c'est le nombre des partie de E si cardE=n+1
donc c'est pas n^[n(n+1)/2]

par **yos** » 04 Juin 2006, 11:28

Le nombre de parties d'un ensemble de (n+1) éléments est

, et je ne vois pas le rapport avec le problème.

par **aviateurpilot** » 04 Juin 2006, 11:35

je voulais dire le nombre des parties qui contien 2 element
parceque si on parle des lois de compositions internes commutatives
on va pas denombrer les couple de E²
on va denombrer le nombre des parties a deux element de E
et c'est n(n-1)/2 avec cardE=n
donc
le nombre de lois internes commutatives sur E est n^[n(n-1)/2]

par **yos** » 04 Juin 2006, 11:48

Je te suggère d'essayer ta formule et la mienne pour n=2, E={a,b}.

par **aviateurpilot** » 04 Juin 2006, 11:55

le nombre de partie dans a 2 elements de {a,b} est 1
et on a 2(2-1)/2 = 1
et ta formule n(n+1)/2 ne donne 3

par **yos** » 04 Juin 2006, 11:59

Je te parle du nombre de lois internes commutatives sur {a,b} : il y en a 8.

par **aviateurpilot** » 04 Juin 2006, 12:02

pour le nombre des lois internes commutative pour E
t'a raison
moi j'ai oublié les a*a
danc c'est n^[(n-1)n/2 +n] = à ta formule pour le nombre des lois commutative

par **yos** » 04 Juin 2006, 12:09

Bien vu!
Tant qu'on y est, quel est le nombre de relations binaires sur E?

par **aviateurpilot** » 04 Juin 2006, 12:11

explique moi d'abord "relations binaires "?

par **yos** » 04 Juin 2006, 12:24

Une relation binaire sur un ensemble E est une partie de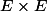

.
Si on appelle R cette relation, on écrit aRb pour dire que a est en relation avec b, ce qui signifie

.
Une fonction (ou application) de E dans E en est un cas particulier. C'est le cas où pour chaque a de E il existe un unique b de E tel que

. On note alors R(a)=b .
On peut le faire aussi de E dans F.

par **aviateurpilot** » 04 Juin 2006, 12:45

si j'ai bien compris

la solution est le nompre des partie de E² - ' l'ensemble vide'
c'est (2^n²)-1
(ca si on supose qu'un element peux n'avoir pas d'image
et que R definie par R(a)=b pour a,b connu de E
est une relation binaire sur E meme s'il ne depend que de 2 element de E et)

Composition interne

composition interne

Qui est en ligne