Composition interne

par **yos** » 04 Juin 2006, 12:52

La relation vide est une relation d'où

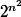
relations sur E.
Combien sont réflexives? symétriques? les deux?
Combien sont antiréflexives? antisymétriques? transitives?
Combien sont des relations d'ordre? d'équivalence?

Définitions sur wikipédia peut-être.

Je reviens ce soir.

par **aviateurpilot** » 04 Juin 2006, 13:03

je vien de connaitre la relation binaires
mais je ne connai pas ca!!!!!!!!!!!!
réflexives? symétriques? les deux?
antiréflexives? antisymétriques? transitives?
des relations d'ordre? d'équivalence?
tu es en quel niveau scolaire??

par **aviateurpilot** » 05 Juin 2007, 11:51

i) $\forall p\in N^*-\{1\},\exists c\in P;\ c\not|p \iff |P|=+\infty$
ii) ||
$\forall (a,b)\in P^2;\ a+b\in P$

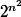
yos a écrit:La relation vide est une relation d'où relations sur E.
Combien sont réflexives? symétriques? les deux?
Combien sont antiréflexives? antisymétriques? transitives?
Combien sont des relations d'ordre? d'équivalence?

Définitions sur wikipédia peut-être.

Je reviens ce soir.

tu te souvien que c'est questions yos ,lol.

réflexives=

symétriques=

les deux=

antisymétriques=

essayons d'etudie tt les relations, meme s'il que tu n'a pas dit

Composition interne

Qui est en ligne