Comment calculer une suite n+1 [Hearsthone]

[Ahima]

Bonjour, merci de me lire, je suis conscient que mon problème est mal formulé mais je n'ai pas suffisamment de connaissances en mathématique, cela m'intéresse néanmoins, d'où ma présence.

Le contexte : un jeu de carte (Hearsthone, genre de jeu "magic" pour ceux qui connaissent, mais en ligne), j'ai déjà réussi le défit mais sans être capable de faire le calcul, et c'est ça qui m'intéresse ici.

Le défit, je dois amener mon ennemie à 0 point de vie, il en a 495.
Je vous passe les détails du jeu qui ne sont pas nécessaires à la compréhension du problème mathématique.
Ce qu'il faut savoir c'est que dans ce défis, je dois me baser sur une mécanique de ce jeu qui consiste à faire piocher des cartes à son adversaire, et comme il n'a plus de carte à piocher, à la place il pioche des dégâts.
La première fois qu'il doit piocher une carte mais qu'il n'en a plus à piocher, il pioche donc 1 point de dégâts.
La deuxième fois il pioche donc 2 points de dégâts et ainsi de suite.
J'arrive à poser qu'il pioche donc un nombre de dégats équivalent au nombre de carte qu'il a pioché, la 18 ème fois il va piocher 18 dégats, la 50 ème 50 dégats.

Ce que j'aimerais c'est que des personnes qualifiées en math me pose le problème comme il se doit.
J'aimerais pouvoir calculer combien de dégats il aura prit en tout à sa 50 ème pioche sans faire 1+2+3+4+5+6 etc +49 +50.
J'aimerais poser l'équation et remplacer une variable par le nombre de pioche pour obtenir le résultat
A cette suite j'aimerais pouvoir calculer combien de fois il devra piocher pour obtenir 495 points de dégats.
Et ce que j'aimerais surtout c'est comprendre la logique du calcul, le résultat m'importe peu.

Pour aller plus loin à chaque fois qu'une créature est soignée, le joueur pioche une carte pour chaque créature qu'il a avec la capacité [quand une créature est soignée, vous piochez une carte]

Comment calculer les différentes possibilités, combien de créatures avec la capacité de pioche doit il posséder pour combien de créature à soigner pour un nombre de pioche donné, j'imagine qu'on peut poser le problème en termes mathématique, sous forme d'une fonction ?

Merci à vous si vous pouvez me transmettre un peu de vos connaissances j'aimerais formaliser tout ça dans mon esprit et être capable de refaire cette démarche tout seul dans un autre cas de figure !

[Ben314]

Salut,
C'est on ne peut plus simple (et bien connu) : si est un entier naturel et alors :

Et, en ajoutant les deux lignes (colonnes par colonnes), il vient que

c'est à dire

Vu qu'il y a termes (égaux) dans la somme.
Donc

P.S. (culturel) Il parait que Carl Friedrich Gauss aurait retrouvé ce résultat alors qu'il été âgé de 9 ans : la légende (réelle ?) dit que son instit., pour avoir la paix pendant un bon moment, avait donné aux élèves à calculer la somme 1+2+3+...+100 et que Gauss aurait répondu (quasi) instantanément...

P.S.2 : selon Wiki, c'est une légende.

[Ben314]

Sinon, ensuite, pour résoudre , on écrit évidement que
- C'est équivalent à
- Donc en multipliant par 2 et en développant le n(n+1) c'est équivalent à
- Là, la "grosse astuce" (*), c'est de dire que c'est "presque" le carré de vu que donc on réécrit l'inéquation sous la forme c'est à dire .
- On prend ensuite la racine carré (les réels considérés sont positifs donc dans le même ordre que leur carré) ce qui donne puis on retranche 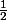des deux cotés :
Donc le plus petit entier solution est 31 (et on peut vérifier que 1+2+3+...+31=496)

(*) Qui, de façon pédante, s’appelle "mise sous forme canonique d'un trinôme du second degré".

Concernant l'histoire des soins et des cartes piochées, j'ai pas suffisamment compris le fonctionnement pour en faire un modèle mathématique.

[Ahima]

[quote="Ben314"]Salut,
C'est on ne peut plus simple (et bien connu) : si est un entier naturel et alors :

Et, en ajoutant les deux lignes (colonnes par colonnes), il vient que

c'est à dire

Vu qu'il y a termes (égaux) dans la somme.
Donc

Merci pour ta réponse !
Je comprends que c'est très basique simple et connu voir trouvable par un enfant de 9 ans mais moi ça ne me parle pas
D'ailleurs je ne comprend pas les calculs que tu me montre.
je ne comprends pas pourquoi tu pars sur des 1+2+3+4+(n-1)
Je croyais que n était égal au n précédent +1 justement ?
Ensuite dans la deuxieme ligne tu finis à rebours s= n + (n-1) + (n+2) +.... + 2 + 1 ?
Pourquoi n-1, pourquoi la ligne fini en avec des chiffres plus petits ?
Je parle même pas des lignes suivantes car je ne comprends pas les deux premières déjà ?
Peut être pourrais tu si tu as le temps m'expliquer la démarche plutôt que de me donner le calcul ?
Merci bien en tout cas

[Ben314]

La démarche, ça me semble plus que difficile de l'expliquer plus en détail que ce que j'ai fait précédemment...
- Dans la première ligne, j'écrit que S=1+2+3+...+n du fait que c'est justement ça qu'on veut calculer donc tout ce que je fait, c'est de donner un nom (à savoir S) à la quantité qu'on désire évaluer.
- La deuxième ligne je vois franchement pas quoi te dire vu que c'est exactement la même que celle du dessus : je n'ai fait que recopier la définition qu'on a pris pour S et c'est tout.
- Et la suivante, ça provient d'un truc qui, me semble-t-il est vu est compris dans le début du primaire : quand on fait une addition, le résultat ne dépend pas de l'ordre dans lequel on fait les calcul. Pour calculer 3+12+7, si on veut on peut commencer par calculer 3+7 (=10) puis ensuite ajouter 12. Donc quand on veut calculer la somme des entiers de 1 à n, on peut commencer par les plus petits : 1 puis 2 puis 3, etc jusqu'à n ou alors commencer par les plus grand : n puis n-1 puis n-2, etc jusqu'à 1.
Bref, en prenant par exemple n=6 et en écrivant tout les termes, on a 1+2+3+4+5+6 = 6+5+4+3+2+1.

[Ben314]

En fait, j'ai bien l'impression que ce que tu comprend pas, c'est le fait qu'en math. on puisse utiliser des lettres pour désigner des nombre (ou alors c'est les poins de suspensions).
Donc je reprend le post avec le cas particulier de n=7 :

Si alors on a :



Et, en ajoutant les deux lignes (colonnes par colonnes), il vient que

c'est à dire

Vu qu'il y a termes (égaux) dans la somme.
Donc

[Yezu]

Merci pour ta réponse !
Je comprends que c'est très basique simple et connu voir trouvable par un enfant de 9 ans mais moi ça ne me parle pas

Je te rassure, le Gauss en question est réputé être un génie et l'un des plus grands mathématiciens ayant existé. Son nom figure dans une MULTITUDE des branches des mathématiques en passant par la physique.
Donc à 9 ans, ce n'est bien évidemment pas trouvable par un gamin ^^

[Ben314]

Et en plus... il semblerait bien que l'anecdote est fausse... (mais c'est vrai que vu le bonhomme, c'était "plausible"...)

Et je reprécise au cas où ça ne soit pas clair que si j'ai mis cette "remarque culturelle", c'est surement pas pour dire que c'est "trouvable à 9 ans". Donc si ça a pu te vexer un tant soit peu, je m'en excuse platement.

[Ahima]

Merci Ben, avec le détail de la progression du raisonnement j'ai saisi.
Ne maniant pas les mathématiques formelles tous les jours effectivement j'ai pas les réflexes de voir que
s= n + (n-1) +(n-2)+(n-3) +(n-4)+(n-5)+(n-6)
c'était pour
s = 7 + (7-1) +(7-2) + (7-3) +(7-4)+(7-5)+(7-6)
pour s= 7+6+5+4+3+2+1
pour s = 1+2+3+4+5+6+7
pour 2s = 8 +8+8+8+8+8+8 = 7*8
pour s=7*8/2
pour s=n(n+1)/2
Même si je sais qu'on peut remplacer un nombre hypothétique par une lettre, et que 1+2+3+4+5 est exactement la même chose que 1+3+5+4+2
C'était justement pour avoir le détail de la progression du raisonnement que je suis venu demander ici !
J'aurais pu trouver le s= n(n+1)/2 sur google mais je voulais comprendre le détail.

C'est souvent que l'on inverse les termes d'un calcul et qu'on additionne les deux lignes en colonnes pour trouver une règle générale (l'équation) ?
C'est ce genre de raisonnement dont j'aimerais percer le mystère car je ne l'aurais pas eu de moi même.

Sinon ne t'inquiète pas au bout de la 4 ème fois j'ai bien compris que tu considères mes lacunes étant du niveau primaire
Je peux t'assurer cependant que beaucoup de choses sont apprises à cet age et pourtant pas nécessairement maîtrisées ou partiellement oubliés si on ne s'en sert pas, comme la différence entre "et" et "est"... la conjugaison du verbe faire au présent première personne du singulier (XD) , certaines habilités sociales pour fonctionner en collectif, etc....

Oui Yezu je sais bien, c'était une boutade pour tenter de faire comprendre que ce qui m’intéressais justement c'était d'apprendre peu importe que mes questions apparemment soient perçus comme stupides.
Enfin, c'est la vie ^^

En tout cas merci bien Ben pour l'explication et le temps consacré c'est très aimable !
Demain je relis la suite de ce que tu m'as écrit sur la "mise sous forme canonique d'un trinôme du second degré" ^^

[Ben314]

C'est souvent que l'on inverse les termes d'un calcul et qu'on additionne les deux lignes en colonnes pour trouver une règle générale (l'équation) ?

Non, c'est pas très fréquent, donc pour la plupart des matheux, ça reste "une astuce" vu qu'il est fort possible de ne pas y penser...
Après, il y a d'autres méthodes pour trouver la valeur de cette somme sans utiliser cette astuce, mais ça demande un bagage mathématique un peu plus important pour bien comprendre les idées alors que là, c'est astucieux, mais les calculs sont très élémentaires (c'est souvent comme ça en math.)

C'est ce genre de raisonnement dont j'aimerais percer le mystère car je ne l'aurais pas eu de moi même.

Demain je relis la suite de ce que tu m'as écrit sur la "mise sous forme canonique d'un trinôme du second degré" ^^

Ca, il y a de forte chance que ça te semble aussi un peu obscur à la première lecture (au niveau scolaire, c'est un bon cran au dessus) et ça va pas être évident de simplifier le bidule en remplaçant le n par une "vrai valeur" vu que justement, la valeur du n, c'est ça qu'on cherche.

[nodgim]

Sinon, une bonne approximation, à partir de ton nombre 495, tu regardes la racine carrée du double, soit ici la racine carrée de 990, donc autour de 31. Après tu testes si 31*32/2 est au dessus ou en dessous de 495.

[fatal_error]

il y a aussi une autre méthode sans trop de bagages:
si jecris

Code: Tout sélectionner

1 2 3 4 5 6 7
1 2 3 4 5 6 .
1 2 3 4 5 . .
1 2 3 4 . . .
1 2 3 . . . .
1 2 . . . . .
1 . . . . . .


si jajoute ligne par ligne le nombre delem je fais
n+n-1+...+1 (qui correspond à S)
et pour compter ben c'est aussi la moitié (du nombre delements) du tableau (incluant la diagonale)
idem n^2/2 sauf que n^2/2 ca divise aussi la diagonale, donc je rajoute la moitié manquante (la diagonale a n éléments..)
S=n^2/2+n/2 (qui en factorisant par n/2 donne)
S=n/2(n+1)

[Ahima]

Salut à tous, merci à vous tous pour votre participation !

Oui nodgim, maintenant que j'ai la formule j'ai fait le calcul de tête et j'ai trouvé au dessous avec 31 et au dessus avec 32, dans mon exemple il aurait fallu lui faire piocher 32 cartes pour gagner.

J'ai pas le temps de regarder maintenant (je reviens tout à l'heure) la suite du calcul donné par Ben à la base mais l'astuce de nodgim j'imagine qu'elle s'explique le détail du calcul développer par Ben ?

A tout à l'heure !