Coeff binomiaux.

[Ben314]

Salut,
Quelle est (en fonction de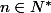 ) la valeur de où les sont les coefficients binomiaux ?

[ffpower]

J'obtiens (-1)^n*n!, mais ma méthode n'est pas, on va dire, fine..
(Je pars de l'identité (1+x)^n=somme des C_n^k*x^k, et j'applique n fois l'opération "je dérive et je multiplie par x" puis j'évalue en -1, sachant qu'à chaque fois que je dérive un produit, la partie ou je ne dérive pas (1+x)^truc peut être laissé de coté car laissera au moins un facteur 1+x à la fin et vaudra donc 0 en -1)

[arnaud32]

(-1)^n*n!
en utilisant les derivees successives de (x+y)^n par rapport a y en (x=1, y=-1). et le binome de newton

[Ben314]

Correct (tout les deux...) :king2:
Aprés, je sais pas s'il y a super plus rapide...
Sauf peut être (à vérifier) en écrivant que, pour compter le nombre de bijections de {1..n} dans lui même, on peut :

- Compter toutes les applications de {1..n} dans lui même ->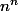
- Enlever celle dont l'image est contenue dans une partie à n-1 éléments de {1..n} ->
- Ajouter celle dont l'image est contenue dans une partie à n-2 éléments de {1..n} -> (vu qu'on les a enlevé deux fois)
etc...

Je pense que ça doit être rédigable "propre" et que ça donne un truc légèrement plus naturel...

Question subsidiaire : d'où elle sort ma somme ? ( comment la "généraliser" ?)