Un classique

par **Zweig** » 06 Mar 2008, 21:08

Soit

une fonction vérifiant :

Montrer que

est constante.

par **ThSQ** » 06 Mar 2008, 22:32

Ouais c'est surement un classique (mais je le connaissais pas).

Ca revient à mettre des valeurs entières dans le plan de façon que chaque case soit la moyenne de ces 4 voisines. Marrant.

Dans le cas discret c'est pas trop dur car on prend la case avec le plus petit nombre (existe forcément). Ces 4 voisins doivent avoir la même valeur nécessairement. Et on "contamine" tout le plan comme ça.

Question naturelle et immédiate : est-ce encore vrai si on remplace IN par IR+ par exemple ?? (on a envie de dire oui mais c'est moins immédiat non ?)

par **Zweig** » 06 Mar 2008, 22:52

Oui, c'est toujours vrai, mais la démonstration est beaucoup plus difficile puisque tu ne peux plus utiliser le principe de l'extremum car un ensemble de réels positifs n'a pas nécessairement de plus petit élément.

par **Imod** » 07 Mar 2008, 12:29

Le problème ( assez connu en effet ) a bien une solution courte mais un "brin" astucieuse . Je donnerais une indication si personne ne trouve :zen:

Imod

par **_-Gaara-_** » 07 Mar 2008, 13:55

Salut,

C'est utile de démontrer qu'elle est paire ?? :hein:

par **Zweig** » 07 Mar 2008, 16:54

Imod > Bah les indications, ThSQ les a données :we:

par **ffpower** » 07 Mar 2008, 17:19

il parlait de la generalisation dans R+ je pense

par **Zweig** » 07 Mar 2008, 17:26

"Dans le cas discret c'est pas trop dur car on prend la case avec le plus petit nombre (existe forcément). Ces 4 voisins doivent avoir la même valeur nécessairement. Et on "contamine" tout le plan comme ça."

par **Imod** » 07 Mar 2008, 19:23

Zweig a écrit:Imod > Bah les indications, ThSQ les a données :we:

En effet , j'ai lu trop vite :marteau: je pensais à la généralisation proposée par ThSQ : je sais le faire quand la fonction est bornée à valeurs réelles .

Imod

par **Zweig** » 07 Mar 2008, 19:26

On avait eu ce problème (le mien) durant un stage d'Animath cet été et le professeur nous donnant le cours (Xavier Caruso pour les connaisseurs) avait oublié la solution si j'ai bonne mémoire. J'aimerais donc voir ta démonstration (si elle est à ma portée).

par **Imod** » 07 Mar 2008, 21:37

Zweig a écrit:J'aimerais donc voir ta démonstration (si elle est à ma portée).

La solution que je connais est de niveau terminale si les TS savent toujours qu'une partie bornée de

a une borne supérieure . Je donnerais ma solution ( ou un indice ) dès que je trouverais un moment entre deux paquets de copies ( je suis un peu débordé en ce moment ) .

Imod

par **lapras** » 07 Mar 2008, 21:43

Mais de toute façon, je ne vois pas le problème vu qu'on a le principe de la borne sup dans IR, ca "remplace" le fait que tout ensemble non vide de IN admet un plus petit élément ?

par **ThSQ** » 07 Mar 2008, 22:51

lapras a écrit:Mais de toute façon, je ne vois pas le problème vu qu'on a le principe de la borne sup dans IR, ca "remplace" le fait que tout ensemble non vide de IN admet un plus petit élément ?

Mmmm, borne inf ne veut pas dire plus petit élément ....

Les extrémums de f ne sont pas forcément atteints sinon c'est de la tarte ( :--: :wc: .....).

par **Imod** » 08 Mar 2008, 19:49

J'ai retrouvé les notes que j'avais prises sur ce problème mais je n'ai pas trop le courage de mettre tout ça au propre . Quelques remarques pouvant aider ceux qui veulent chercher ( sinon il faudra attendre un peu pour la solution ). Une fonction bornée

de

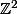dans

est dite harmonique si :

. L'ensemble des fonctions harmoniques est un espace vectoriel sur

contenant les constantes . De plus si

est harmonique alors

est aussi harmonique . En supposant

non constante , je vous laisse trouver une contradiction :zen:

Imod

par **Imod** » 12 Mar 2008, 19:36

J'ai ouvert un sujet similaire sur le site Les Mathématiques.net ( Domi=Imod ) J'invite ceux que ça intéresse à y jetter un coup d'oeil :zen:

Imod

Mathematiques.net

par **ThSQ** » 12 Mar 2008, 21:19

Imod a écrit:De plus si est harmonique alors est aussi harmonique .

:+++: Waouh ... Fallait y penser :dingue2:

par **ffpower** » 13 Mar 2008, 05:05

chui en train de réfléchir avec un pote sur cet exo(dans le cas général bien sur^^).Ché pas si ca peut aider mais je crois avoir réussi a montrer qu une fonction harmonique positive était forcément a croissance linéaire

par **jugurthamoi** » 13 Avr 2008, 00:15

salut, regardez ce truc... qu'en pensez-vous ?
On commence par développer tous les termes un à un :

.f(x-1,y)=f(x-2,y)+f(x-1,y+1)+f(x,y)+f(x-1,y-1)
.f(x,y+1)=f(x-1,y+1)+f(x,y+2)+f(x+1,y+1)+f(x,y)
.f(x+1,y)=f(x,y)+f(x+1,y+1)+f(x+1,y-1)+f(x+1,y-1)
.f(x,y-1)=f(x-1,y-1)+f(x,y)+f(x+1,y-1)+f(x,y-2)

En sommant tous les membres, j'obtiens à gauche :la formule de définition, à droite j'ai une somme bizarre mais avec 4f(x,y) .

En simplifiant il reste 0=f(x-2,y)+ ...+f(x+1,y+1)+...+f(x,y-2).
Comme f est dans N alors la somme de termes positifs est nulle ssi chaque terme est nul. En particuler: f(x+1,y+1)=0.
or si je pose p=x+1 et q=y+1 sont dans Z donc:
pour tout p,q dans Z:
f(p,q)=0

Conclusion: f est identiquement nulle.

par **ffpower** » 13 Avr 2008, 02:43

T as oublié les 4 devant les termes de gauche.ce serait trop facile^^.Cela dit ca permet d exprimer f(x,y) comme la moyenne de f sur un contour un peu plus grand. c est comme ca que j ai d ailleurs reussi a obtenir la croissance sous linéaire de f...

par **jugurthamoi** » 13 Avr 2008, 11:25

Oups! :briques: t'as raison. je l'ai fait a une heure du matin, faut que j'arrette de bosser a cette heure là ...

Un classique

Un classique

Qui est en ligne