Donc voilà mon plan de demo :
Je pars de
)
et
)
comme dans l'énoncé en supposant de plus que
)
et
)
sont injectives, que
)
commence et finit sur la même verticale(
=p_1(M_m))
), et que
)
commence et finit sur la même horizontale (
=p_2(N_n))
). Il est facile de se ramener à ce cas.
Je dirai que
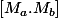
est un demitour de longueur b-a de
)
si
=p_1(M_{a+1})=....=p_1(M_b))
, et
=p_1(M_{b+1}))
, et
\not=p_1(M_{a-1}).)
.ou si on la même chose en remplacant

par
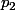
.. ( autrement dit,
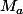
et
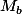
sont des coins consécutifs ou le chemin tourne 2 fois dans la meme direction ).
Supposons maintenant que
)
et
)
ne se croisent pas. Si
)
et
)
ne sont pas tous 2 des lignes droites ( cas trivial ), il y a forcément des demis tours effectués. J'en choisis un de longueur minimale, disons
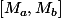
. On constate alors qu'entre les points
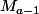
et
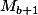
, il n'y a aucun point de
)
ni de
)
, car ceci impliquerait l'existence d'un demi tour de longueur plus petite. Du coup, on peut construire un nouveau chemin
)
, identique à
)
, sauf qu'au lieu de tourner en
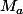
puis en
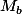
, on tourne en
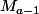
puis en
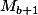
. Ainsi
)
et
)
vérifie encore les mêmes hypotheses, et
)
est plus court que
)
( de 2 cases ). Donc en itérant le procédé, on finit par se ramener au cas trivial des 2 droites..
PS : c'est dans ce genre de situation que je regrette de ne pas savoir maitriser d'outils de dessins comme vous. J'espere que vous arriverez quand même à suivre la démarche..
EDIT :
Ben314 a écrit:Bon, désolé : je suis à la fac et j'ai rien sous format informatique en topo algébrique...
Pas bien grave, merci quand même..Le lien que tu m'as passé me va de toute facon très bien pour l'instant..

