Chemins sur un échiquier

[Imod]

En fin de compte il me semble qu'on peut régler le problème tout bêtement par l'absurde . Notons P(m,n) la propriété : dans un échiquier mXn il existe deux chemins HB et GD n'ayant aucune case commune et supposons cette propriété vraie pour au moins un couple (m,n ) . Munissons l'ensemble des couples (m,n) de l'ordre lexicogaphique et choisissons (m,n) minimum tel que P(m,n) soit vraie ((m,n) est différent de (1,1)) . On peut alors supprimer une ligne ou une colonne de cet échiquier (m,n) en conservant deux chemins sans case commune ce qui contredit la minimalité du couple (m,n) .

Imod

[vincentroumezy]

On peut dire que le chemin de chaque pion est continu.
On a donc une courbé continue de haut en bas et une autre de gauch à droite. Aucune des deux courbes ne pouvant etre contournée, elle sera forcément coupée par l'autre.La courbe "verticale" sépare l'échiquier en deux parties, une gauche et une droite contenant l'une le bord gauche, l'une le bord droit. L'autre pion les relie, et coupe donc la courbe verticale de séparation.

[ffpower]

Merci d'avoir up :we:
C'est effectivement une discretisation de la version continue. Cela dit la version continue n'est pas plus simple. Car essaie d'écrire mathématiquement que "la courbe ne peut pas être contournée". Tu peux faire tous les TVI que tu veux, je te parie un pastis que ca n'aboutira pas^^

[vincentroumezy]

Le plan est limité a un carré ont deux bords sont reliés par une courbe continue.La contourner signifie ne pas la traverszr pour aller de gauche à droite.Pour traverser ce morceau de plan , il faut couper la courbe continue pour ne pas sortir du carré.

[ffpower]

D'ac, mais comment tu justifies rigoureusement alors qu'on ne peut pas "contourner" la courbe?

[nodjim]

Ouais. Autant demander de prouver qu'une ligne droite est droite. Je vois trop où est le problème. Le tracé de droite à gauche coupe le plan en 2 demi plans, le haut et le bas, quel que soit le tracé et ses contours, détours, tortillonnades. Je ne vois quelle rigueur tu veux en plus.
Comprends pas ton hésitation.

[vincentroumezy]

Si je n'ais pas été clair:
Le carré est dLe projeté othogonal de la courbe qui va de haut en bas est le coté du carré.
Sa hauteur est n.
La courbe qui va de gauche à droite a une "amplitude" de hauteur maximum de n.
Elle ne peut pas monter ou descendre à des hauteurs qui lui donneraient une amplitude supérieure à n.
C'est ce que j'appellr contourner, et c'est donc impossible.

[Imod]

Ce problème est intuitivement évident donc toute preuve qui dit que c'est évident qu'on a ceci ou cela n'est pas recevable .

Imod

[Ben314]

Salut, à force de cogiter, j'ai bien une solution, mais elle est (au départ) de "haut niveau", mais je pense qu'on peut la présenter (surtout dans le cas discret) à un niveau plus bas.
Un outil assez puissant qui "étend" assez bien le Théorème des Valeurs Intermédiaires à la dimension 2 est la notion d'indice d'un point par rapport à une courbe (continue et fermée, c'est à dire dont le point de départ est le même que le point d'arrivé).
Pour ceux qui ne connaissent pas la notion voila une des façons de définir l'indice (il y en a d'autres) :
On a une courbe paramétrée (continue)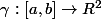 et un point non situé sur la courbe.
On peut démontrer qu'il existe une paramétrisation de la courbe en coordonnées polaires centrées en , c'est à dire des fonctions continues 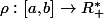et 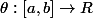telles que, pour tout 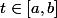le vecteur ait pour coordonnées .
Comme , on a donc est un entier et c'est lui que l'on apelle "indice du point par rapport à la courbe " et que l'on peut par exemple noter .
Il est bon de noter que la fonction est clairement unique, que la fonction ne l'est pas (on peut la décaler de 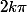) mais que la valeur de ne dépend pas du choix de la fonction . On peut aussi montrer (facile) que l'indice ne dépend pas de la paramétrisation de la courbe choisie : c'est une vrai "notion géométrique".
Si on fait un petit dessin, on voit que, graphiquement parlant, l'indice de par rapport à , c'est le "nombre de tours que fait la courbe autour de ".
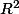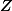Une autre chose (relativement) façile à montrer, c'est que la fonction définie sur privé du support de et à valeur dans est continue donc constante sur chaque composante connexe du complémentaire de la courbe. En fait, on a donc à peu de frais un résultat un peu de même nature que le théorème de Jordan.

Par rapport au problème de départ (version continue) : on part d'une courbe continue qui va d'un point du haut de l'échiquier a un point du bas (et ne passant par aucun point du bord droit ou gauche). On en fait une courbe fermée en rajoutant une large boucle passant à l'extérieur de l'échiquier, par exemple par la droite. Il est facile de montrer que, par rapport à cette courbe, les points du bord gauche de l'échiquer ont un indice de +1 alors que ceux du bord droit ont un indice de 0. Il ne sont donc pas dans la même composante connexe du complémentaire de la courbe et cela signifie que l'on ne peut pas aller du premier point au second sans couper la courbe.
C.Q.F.D.

P.S. S'il y en a des courageux, un petit "défi" :
Comment "discrétiser" le mieux possible cet argument dans le cas de "cases" de l'échiquier (il faudrait trouver un "truc" pas trop compliqué, définit sur chaque case ne faisant pas parti du trajet du premier pion, qui soit invariant lorsque l'on passe d'une case à une de ces voisine et qui ne prenne pas la même valeur pour les cases du bord droit et du bord gauche...)

[Doraki]

Le problème est de donner une vraie fonction concrète qui soit facilement calculable qui dise si on est à gauche ou à droite de la courbe.

Si on le chemin est donné avec un sens de parcours, donc sous forme d'une suite de cases contiguës.
Si (x,y) n'est pas une case du chemin, soit f(x,y) = la parité du nombre de liaisons (x',y) <-> (x',y+1) avec x'
Alors on peut prouver sans trop d'effort que f est localement constante (2 cases qui ne sont pas dans le chemin et qui sont voisines (même en diagonale) prennent la même valeur par f)
Et, quitte à élargir un peu l'échiquier, que le "bord gauche" et le "bord droit" prennent des valeurs différentes.

Et si on veut, on peut faire une récurrence sur y pour montrer que à y donné, les liaisons (x',y) <-> (x',y+1), quand on les range pour des valeurs de x croissantes, elles se font dans des directions alternées.

Evidemment, dans le cas continu, c'est plus dur, et je sais pas comment on fait d'ailleurs.

edit : j'ai raté de répondre à la question de Ben avant qu'il la poste.

[ffpower]

Bonjour,
l'argument de Ben marche clairement..Mais j'aurais justement aimé éviter l'emploi de ce genre d'outils. Si on arrive à obtenir une version discrete de cette démo, ok ça pourrait être bien.

En l'occurence, c'est un peu ce que fait Doraki ( essayer de définir un espece d'indice discret ). Donc je vais vérifier sa preuve de ce pas, voir s'il n'aurait pas omis "des cas foireux" ( y en a souvent^^ )

PS: le cas continu est facilement impliqué par le cas discret : il suffit de faire des quadrillages de plus en plus fins, regarder les chemins sur le quadrillage induits par nos chemins continus, d'appliquer le théo version discrete, et de conclure par un argument de compacité..

[Doraki]

Je veux bien voir un quadrillage qui approxime bien une courbe comme f(t) = (t*cos(1/t), t*sin (1/t)) pour t <>0, f(0) = (0,0).

[Imod]

Assez d'accord et j'aime bien l'inversion de pouvoir qu'on est en train de vivre : le discret face au continue .

Je n'ai rien contre l'analyse et ses magnifiques résultats , mais bon :we:

Imod

[nodjim]

En fait, la question que je me pose: Si un pion fait sa traversée complète avant l'autre, alors on admettrait l'évidence du croisement. Si les 2 pions se déplacent en même temps, c'est là qu'on n'est pas sûr ?

[Doraki]

Si un pion fait sa traversée complète avant l'autre, alors on admettrait l'évidence du croisement.

Non non.

Et puis "les pions se déplacent en même temps" ça veut rien dire si tu les autorise à rester sur place ou à tourner en rond dans un coin pendant que l'autre bouge.

[Ben314]

DORAKI = Trés Trés FORT (en particulier, le fait il réponde à une question qu'on pose... avant qu'on pose la question... :ptdr: )

[nodjim]

C'est bien donc là que je ne vous suis pas. Vos subtilités m'échappent.
On peut toujours dessiner le contour extérieur du cheminement d'un pion, comme un polygone de points. Ce contour continu traverse de part en part l'échiquier. Il doit donc être forcément franchi par le second pion.

[Doraki]

pourquoi est-ce qu'il doit être forcément franchi ?
pourquoi est-ce que si on a un échiquier dont on recolle les bords (donc une sorte de cylindre), le deuxième pion na va plus forcément franchir ?

[ffpower]

Je veux bien voir un quadrillage qui approxime bien une courbe comme f(t) = (t*cos(1/t), t*sin (1/t)) pour t 0, f(0) = (0,0).

Mon "chemin induit" était certes pas une bonne maniere de voir les choses : avec des fonctions de ce genre ca risque en effet de passer par une infinité de cases. Faut plutot regarder le truc comme ca en fait : l'ensemble des chemins affines par morceaux, constitués uniquement d'un nombre fini de traits verticaux et horizontaux de longueurs rationnelles sont dense dans l'ensemble des chemins continus, et correspondent à un chemin discret sur un quadrillage bien choisi..

Imod : tu connais la démo de Brouwer par le lemme de Sperner? Si ce n'est pas le cas, ça devrait te plaire ( fait dans Raisonnements divins/Proofs from the book en dim 2 mais assez aisément généralisable en dim n..)

[vincentroumezy]

Voila. On fait ce qu'on peut.