Chemins sur un échiquier
Cela fait un moment que j'ai envie d'en savoir plus sur la théorie des graphes,
mais pour ça faudrait que j'arrète de bavarder sur le web.
Quoique.
Pour l'autre partie celle défendue par nodjim, je m'en tape un peu.
J'ai juste consolidé le moral des troupes parce que face à Ben, Doraki et ffpower, je trouve que c'est pas très équilibré, mème si nodjim est un grand garçon.
Alors pour qu'il puisse continuer, encore un peu d'huile sur le feu:
On montre que la droite droite qu'avance tout droit de gauche à droite sépare l'échiquier en 2 ou 3 parties:
partie du haut
la droite colorée en rouge
partie du bas
On montre que la ligne brisée qui ne se recoupe pas est équivalente à la droite, c'est une droite froissée, suffit de la défroisser en tirant sur les bouts.
On montre que les boucles lors des recoupes de la ligne brisée, ces boucles isolent des territoires annexés en rouge.Alors si on défroisse les brisures on obtient , on retombe sur la droite avec sur cette droite des verrues correspondants aux boucles, mais en terme de frontière c'est idem la droite.
A toi demain nodjim , fait tout péter ...
mais pour ça faudrait que j'arrète de bavarder sur le web.
Quoique.
Pour l'autre partie celle défendue par nodjim, je m'en tape un peu.
J'ai juste consolidé le moral des troupes parce que face à Ben, Doraki et ffpower, je trouve que c'est pas très équilibré, mème si nodjim est un grand garçon.
Alors pour qu'il puisse continuer, encore un peu d'huile sur le feu:
On montre que la droite droite qu'avance tout droit de gauche à droite sépare l'échiquier en 2 ou 3 parties:
partie du haut
la droite colorée en rouge
partie du bas
On montre que la ligne brisée qui ne se recoupe pas est équivalente à la droite, c'est une droite froissée, suffit de la défroisser en tirant sur les bouts.
On montre que les boucles lors des recoupes de la ligne brisée, ces boucles isolent des territoires annexés en rouge.Alors si on défroisse les brisures on obtient , on retombe sur la droite avec sur cette droite des verrues correspondants aux boucles, mais en terme de frontière c'est idem la droite.
A toi demain nodjim , fait tout péter ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Ben314 a écrit:Je ne sais pas trop ce que tu appelle "dénigré en france", mais je connais pas mal de monde (chercheurs) qui utilisent depuis de nombreuses années des graphes pour modéliser certains groupes issus de considérations géométriques.
Je te parle d'il y a 30 ans , aujourd'hui les choses ne sont plus tout à fait les mêmes , les graphes sont enseignés au lycée dans certaines sections .
Imod
On reprend, je vais bientot changer de pseudo et laisser beagle pour pitbull.
Théorie des graphes.
Le trajtet en ligne continue brisée non sécante de gauche à droite isole 3 surfaces:
-H=haut
-C=courbe
-B=bas
Ligne droite ou ligne brisée non sécante c'est idem,
courbe= épaissseur 1 case (on peut mettre les points de départ haut et bas
il y a WXYZ (j'avais mis ABCD, mais C et B sont déjà pris) coins de l'échiquier et EF à gauche, GH à droite,
la surface C est délimitée par bords de l'échiquier EF,GH et EG et FH.
ligne droite ou ligne brisée c'est idem en terme de chemins et donc de surfaces
Ensuite ne reste plus que le cas des boucles, la ligne brisée se recoupe elle-mème, et on montre que une boucle ramène à C ( courbe)+ plus D nouvelle surface, D est prise sur la surface de H ou B ne gène pas la progression de C qui restera d'épaissseur 1 case et ira par ligne brisée non sécante de bord gauche à bord droit.
On montre que deux ou n boucles donnent un nombre supplémentaire de surfaces dont il n'est pas besoin de tenir le décompte,ni les surfaces
car seule la ligne C nous intéresse,son existence dans tous les cas de figure rend impossible le passage de H vers B.
Dans la démo boucle, il y a de légères variantes avec semi-boucles qui seront des boucles (c'est juste pour garder une C d'épaisseur 1 case.
l'idée de garder C à une case ligne brisée , c'est qu'ainsi les chemins EG et FH restent sans embrouilles.
Théorie des graphes.
Le trajtet en ligne continue brisée non sécante de gauche à droite isole 3 surfaces:
-H=haut
-C=courbe
-B=bas
Ligne droite ou ligne brisée non sécante c'est idem,
courbe= épaissseur 1 case (on peut mettre les points de départ haut et bas
il y a WXYZ (j'avais mis ABCD, mais C et B sont déjà pris) coins de l'échiquier et EF à gauche, GH à droite,
la surface C est délimitée par bords de l'échiquier EF,GH et EG et FH.
ligne droite ou ligne brisée c'est idem en terme de chemins et donc de surfaces
Ensuite ne reste plus que le cas des boucles, la ligne brisée se recoupe elle-mème, et on montre que une boucle ramène à C ( courbe)+ plus D nouvelle surface, D est prise sur la surface de H ou B ne gène pas la progression de C qui restera d'épaissseur 1 case et ira par ligne brisée non sécante de bord gauche à bord droit.
On montre que deux ou n boucles donnent un nombre supplémentaire de surfaces dont il n'est pas besoin de tenir le décompte,ni les surfaces
car seule la ligne C nous intéresse,son existence dans tous les cas de figure rend impossible le passage de H vers B.
Dans la démo boucle, il y a de légères variantes avec semi-boucles qui seront des boucles (c'est juste pour garder une C d'épaisseur 1 case.
l'idée de garder C à une case ligne brisée , c'est qu'ainsi les chemins EG et FH restent sans embrouilles.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Je pense qu'il est possible qu'il n y ait jamais de frontière intérieure.
Toute portion du carré entourée par la courbe est annexée au territoire.
La frontière extérieur est u contour, c'est à dire une courbe qui fait le tour du territoire, en ayant àsur un de ses cotés le territoire vide, et de l'autre, le territoire tracé
Toute portion du carré entourée par la courbe est annexée au territoire.
La frontière extérieur est u contour, c'est à dire une courbe qui fait le tour du territoire, en ayant àsur un de ses cotés le territoire vide, et de l'autre, le territoire tracé
ffpower a écrit:Ben imagine qu'avant de boucler, le pion fasse des chemins alambiqués comme sur le dessin ( qui certes, ne correspond pas EXACTEMENT au contexte, mais un peu d'imagination que diable^^), comme reconnaitre ce qui est à l'exterieur de ce qui est à l'interieur? On a juste déplacé le probleme, une fois de plus (inutilement d'ailleurs, vu que ca sert à rien de reconnaitre les zones interieures, mais bon )
Je l'ai dit, en teintant en rouge le territoire, on sait immédiatement si un point quelconque est dans ou hors du territoire. La complexité du dessin n'est pas un obstacle quand on a compris l'unicité du territoire.
Doraki a écrit:Parceque au fond de moi j'ose espérer que toi quand tu regardes un territoire, tu as une méthode pour déterminer cette chose étrange que tu appelles "frontière extérieure", et si par exemple, tu prenais le soin de nous décrire cette méthode, ça nous en donnerait une définition et on pourrait continuer.
Pour tracer la frontière extérieure: on prend au départ les 2 points du territoire les + éloignés l'un de l'autre.Ces 2 points sont sur la frontière extérieure (facile à prouver). Pour dessiner le contour: on peut, par exemple, à partir d'un de ces points, dessiner, dans le territoire, et sur le bord, un trait continu: on prend un sens arbitraire et on suit toujours le bord main gauche par exemple. Est ce qu'on ne fera pas le tour complet du territoire et est ce qu'on ne reviendra pas au point de départ ?
Les boucles, c'est pas ça le problème :
Tu part d'une courbe C, tu enlève les boucles et tu obtient une courbe C' qui évidement est contenue dans C donc si tu arrive à montrer que C' sépare en au moins deux morceaux cela prouvera que C sépare aussi en au moins deux morceaux.
Par contre le problème c'est ça :
Tu part d'une courbe C, tu enlève les boucles et tu obtient une courbe C' qui évidement est contenue dans C donc si tu arrive à montrer que C' sépare en au moins deux morceaux cela prouvera que C sépare aussi en au moins deux morceaux.
Par contre le problème c'est ça :
Comment montre tu qu'une ligne brisée "toute pourrie" (style celle du post de ffpower) c'est "idem" qu'une ligne droite ?beagle a écrit:Ligne droite ou ligne brisée non sécante c'est idem...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:Les boucles, c'est pas ça le problème :
Tu part d'une courbe C, tu enlève les boucles et tu obtient une courbe C' qui évidement est contenue dans C donc si tu arrive à montrer que C' sépare en au moins deux morceaux cela prouvera que C sépare aussi en au moins deux morceaux.
Par contre le problème c'est ça :
Comment montre tu qu'une ligne brisée "toute pourrie" (style celle du post de ffpower) c'est "idem" qu'une ligne droite ?
la première chose est de ne pas se laisser enfermer dans le merdier de ffpower,
la solution est ètre l'architecte, et construire soi-mème.
Donc la surface C est délimitée par EF et GH sur les bords de l'échiquier,
et les deux chemins EG et FH qui seront , qui resteront bien individualisés pendant toute la construction du parcours.
Donc on part de EF,
on avance une case, cela forme G' et H' les furturs G et H.
tant que ligne brisée non sécante les chemins EG' et FH' sont nets, cleans
3 situations peuvent brouiller=
-des retours dans la courbe, ascenseurs,
ces cases sont éliminées de C,
on reprend le chemin à partir de là
ex: b3c3c4c5c6c7d7d8d7c7c6c5c4
surface C est constituée de b3c3c4
sont éliminés de C c5c6c7d7d8d7c6c5
-des collages exemple:
a3b3c3d3d4c4b4:
forme C le chemina3b3b4
sont éliminés de c c3d3d4c4
- des boucles plus complètes:
la boucle est éliminée de C,
C continue à partir de la case commune:
exemple
a3b3c3d3d4d5c5b5b4b3
est constitutif de C:a3b3
sont éliminés de C c3d3d4d5c5b4
Ainsi il est possible de progresser pour que le jeu se termine lorsque G'=G et H'=H lorsqu'on arrive sur le bord droit de l'échiquier.
Au total il existe:
un espace C nettement délimité par les chemin EG et FH et partout d'épaisseur 1 case.
dans les espaces appelés H=haut et dans les espaces appelés B= bas
on trouvera des cases de passage normalement infranchissables,
mais c'est du bonus en gène, donc je ne les répertorie pas, ni en nombre, ni en superposition, ni en rien,
on s'en fiche.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Soit un repère du plan. O est le coin inférieur gauche de l'échiquier. On gradue les axes de 0 à x. Pour tout altitude h, le territoire tracé par le pion est compris entre les points d'abcisse a et a', avec a'>a.
Après avoir tournicoté, la courbe de l'autre pion arrive au point d'abcisse c< c' le point du territoire rouge situé à la meme altitude h2
La courbe veut atteindre le point situé à une hauteur quelconque h' d'abcisse d>d', ou d' est l'abcisse du point du territire du pion à la trajectore verticale.
L'autre pion doit donc aller du point de coordonnées c et h2, à celui de coordonnées d et h'.
Comme la courbe qu'il décrit est continue, il devra traverser tous les points qui se trouve surla le segment qui relie ces deux points.
Il devra donc traverser le territoire décrit par le pion de couleur rouge.
Après avoir tournicoté, la courbe de l'autre pion arrive au point d'abcisse c< c' le point du territoire rouge situé à la meme altitude h2
La courbe veut atteindre le point situé à une hauteur quelconque h' d'abcisse d>d', ou d' est l'abcisse du point du territire du pion à la trajectore verticale.
L'autre pion doit donc aller du point de coordonnées c et h2, à celui de coordonnées d et h'.
Comme la courbe qu'il décrit est continue, il devra traverser tous les points qui se trouve surla le segment qui relie ces deux points.
Il devra donc traverser le territoire décrit par le pion de couleur rouge.
Ben, pour être honète, je comprend que dalle ni à l'un, ni a l'autre : il y a des tonnes de trucs "pas définis" :
@beagle : dés la première ligne, tu parle de "la surface C" : c'est qui ?
De plus, je comprend même pas ce que tu cherche à montrer...
Il semblerait que tu veut prouver un truc par récurrence, mais j'ai beau avoir lu 4 fois ta preuve, je vois vraiment pas quoi...
@vincentroumezy : c'est quoi le c' ? c'est quoi le "territoire rouge" ? je comprend pas non plus l'argument "il devra traverser tous les points qui se trouve sur le segment qui relie ces deux points" : ça donne l'impression que tu considère que la seule façon d'aller d'un point à un autre est la ligne droite...
@beagle : dés la première ligne, tu parle de "la surface C" : c'est qui ?
De plus, je comprend même pas ce que tu cherche à montrer...
Il semblerait que tu veut prouver un truc par récurrence, mais j'ai beau avoir lu 4 fois ta preuve, je vois vraiment pas quoi...
@vincentroumezy : c'est quoi le c' ? c'est quoi le "territoire rouge" ? je comprend pas non plus l'argument "il devra traverser tous les points qui se trouve sur le segment qui relie ces deux points" : ça donne l'impression que tu considère que la seule façon d'aller d'un point à un autre est la ligne droite...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Soit une ligne droite de passage de pion de case en case qui part de la gauche de l'échiquier et arrive à la droite de l'échiquier.
Elle démarre puisqu'elle a une épaisseur de 1 case d'échiquier,
d'un point supérieur gauche:E
d'un point inférieur gauche:F
elle se termine à droite par un point sup droit : G
un point inférieur droit :H
Avec le carré de l'échiquier, on définit ainsi 3 surfaces:
-H=haut
-C=courbe de déplacement d'épaisseur 1 case:limites sont latérales EF et GH, limite sup:EG, limite inf:FH
-B=bas
Le chemin supérieur qui va de E vers G, s'appelle EG
Le chemin inférieur qui va de F vers H, s'appelle FH
Un chemin peut étre une ligne droite ou une ligne brisée.
j'ai défini 3 situations de géne au repérage de ces chemins,
mais en construisant le chemin de gauche à droite les chemins EG' et FH'
sont bien définis en dehors de ces situations
raison pour laquelle je veux garder du début à la fin, une épaisseur de 1 seule case.
Et chemin sup ne coupant jamais chemin inf, je reste avec UNE seule surface C du début à la fin
...
Elle démarre puisqu'elle a une épaisseur de 1 case d'échiquier,
d'un point supérieur gauche:E
d'un point inférieur gauche:F
elle se termine à droite par un point sup droit : G
un point inférieur droit :H
Avec le carré de l'échiquier, on définit ainsi 3 surfaces:
-H=haut
-C=courbe de déplacement d'épaisseur 1 case:limites sont latérales EF et GH, limite sup:EG, limite inf:FH
-B=bas
Le chemin supérieur qui va de E vers G, s'appelle EG
Le chemin inférieur qui va de F vers H, s'appelle FH
Un chemin peut étre une ligne droite ou une ligne brisée.
j'ai défini 3 situations de géne au repérage de ces chemins,
mais en construisant le chemin de gauche à droite les chemins EG' et FH'
sont bien définis en dehors de ces situations
raison pour laquelle je veux garder du début à la fin, une épaisseur de 1 seule case.
Et chemin sup ne coupant jamais chemin inf, je reste avec UNE seule surface C du début à la fin
...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
Tu (on) tourne en rond : comment prouve tu qu'il y a bien trois surfaces, c'est à dire qu'il est impossible d'aller de haut en bas sans couper ?beagle a écrit:Avec le carré de l'échiquier, on définit ainsi 3 surfaces
Le problème n'est pas de définir les chemins, c'est de montrer qu'ils séparent en plusieurs zones.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
salut,
une tentative:
x et y représentent des variables au pif pour les indices de la matrices, les indices des variables au pif différentes de x et y.
des variables au pif différentes de x et y.
notons) , la matrice dont
, la matrice dont  est lindice ligne, et
est lindice ligne, et  la colonne. Donc
la colonne. Donc  entre 1 et n, et
entre 1 et n, et  aussi.
aussi.
Soit) l'hypothèse : dans un rectangle de largeur (end-first) partant d'une case
l'hypothèse : dans un rectangle de largeur (end-first) partant d'une case ) et atteignant
et atteignant ) pour le pion 1, alors le pion 2 passe par une des cases surlaquelle était le pion 1.
pour le pion 1, alors le pion 2 passe par une des cases surlaquelle était le pion 1.
 )si il existe un chemin
)si il existe un chemin ...A(x_2,y_p)) et que celui-ci vérifie
et que celui-ci vérifie ) , noté
, noté  , alors quelquesoit un point
, alors quelquesoit un point ) relié à
relié à  ,
, ) reste vérifiée.
reste vérifiée.
 )si il existe un chemin
)si il existe un chemin ...A(x_2,y_p)) noté
noté  vérifiant
vérifiant ) , et qu'il existe le chemin
, et qu'il existe le chemin A(x_2,y_{p+1})) alors
alors ) est aussi vérifiée.
est aussi vérifiée.
Lorsqu'un chemin vérifie) nous dirons que celui-ci présente la propriété "infranchissable pour
nous dirons que celui-ci présente la propriété "infranchissable pour ) ".
".
démo de :
:
Soit le chemin construit.
le chemin construit. ) relié à
relié à  signifie il existe
signifie il existe ) ,
,  , appartenant à
, appartenant à  tel que il existe
tel que il existe A(...)A(joinX,joinY)) . A(...) représente autant de cases en moins inaccessibles pour le pion 2.
. A(...) représente autant de cases en moins inaccessibles pour le pion 2.  vérifie toujours
vérifie toujours ) .
.
démo de :
:
 est infranchissable pour
est infranchissable pour ) . Rajoutons la colonne p+1.
. Rajoutons la colonne p+1. 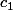 le chemin
le chemin ) .
.  étant infranchissable, seul
étant infranchissable, seul A(x_2,y_{p+1})) peut être franchis.
peut être franchis.
Or) et
et ) étant cote à cote,
étant cote à cote,  ne peut pas franchir
ne peut pas franchir A(x_2,y_{p+1})) donc ne peut pas non plus franchir
donc ne peut pas non plus franchir 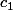 .
.
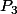 )Si il existe
)Si il existe  (un chemin reliant deux points), il existe au moins une transition
(un chemin reliant deux points), il existe au moins une transition ) , pour j=1 à n-1, qui est par
, pour j=1 à n-1, qui est par
définition infranchissable, appartenant toutes à .
.
démo de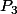 :
:
on commence en) et on veut aller en
et on veut aller en ) , avec notre premier pion.
, avec notre premier pion.
Pour aller en) il est nécessaire d'être en
il est nécessaire d'être en ) (seule la n-1 colonne est en relation avec la neme).
(seule la n-1 colonne est en relation avec la neme).
Par récurrence, le pion va accéder à chacune des colonnes.
Démo de) :
:
Par récurrence
Initialisation:
montrer que : pour tout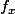 ,
,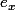 , il existe un chemin noté
, il existe un chemin noté  tel que
tel que A(e_x,2)) qui vérifie
qui vérifie ) .
.
il existeA(e_x,2)) donc d'apres
donc d'apres 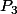 , il existe
, il existe ) appartenant à
appartenant à  .
.
) est infranchissable et représente un chemin
est infranchissable et représente un chemin A(inf_x,2)) .
.
soit) est reliée au chemin
est reliée au chemin A(inf_x,2)) , donc l'ensemble
, donc l'ensemble ...A(inf_x,1)A(inf_x,2)) reste infranchissable d'après
reste infranchissable d'après  .
.
De même pour...A(inf_x,1)A(inf_x,2)A(f_y,2)) et donc
et donc ) est vraie pour tout
est vraie pour tout  .
.
Hérédité faite sur p:
) est vraie, démontrer
est vraie, démontrer ) .
.
Il existe un chemin...A(x_{p+1},p+1))
Soit >un< chemin vérifiant
>un< chemin vérifiant ) . (
. ( infranchissable pour
infranchissable pour ) )
)
Soit) qu'on veut connecter à
qu'on veut connecter à  .
.
Soit E l'ensemble des points appartenant à en colonne p (
en colonne p ( \in c_0\}) )
)
Donc d'après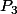 , il existe
, il existe ) avec un certain
avec un certain 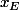 elem de E et
elem de E et )
Le cheminA(x_E,p+1)) est par définition infranchissable.
est par définition infranchissable.
Par ailleurs rappelons que) est vraie pour tout chemin possèdant un elem
est vraie pour tout chemin possèdant un elem ) . Posons
. Posons  un de ces chemins.
un de ces chemins.
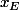 appartient donc à ce
appartient donc à ce  , et est de colonne
, et est de colonne  .
. ) reste vérifiée.
reste vérifiée.
D'après ,
, 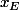 appartient à
appartient à  vérifiant
vérifiant ) et
et A(x_E,p+1)) existe donc
existe donc ) est vérifiée.
est vérifiée.
Donc pour tout n,) est vérifiée et donc le pion2 passe par une case sur laquelle était le pion 1.
est vérifiée et donc le pion2 passe par une case sur laquelle était le pion 1.
une tentative:
x et y représentent des variables au pif pour les indices de la matrices, les indices
notons
Soit
Lorsqu'un chemin vérifie
démo de
Soit
démo de
Or
définition infranchissable, appartenant toutes à
démo de
on commence en
Pour aller en
Par récurrence, le pion va accéder à chacune des colonnes.
Démo de
Par récurrence
Initialisation:
montrer que : pour tout
il existe
soit
De même pour
Hérédité faite sur p:
Il existe un chemin
Soit
Soit
Soit E l'ensemble des points appartenant à
Donc d'après
Le chemin
Par ailleurs rappelons que
D'après
Donc pour tout n,
la vie est une fête 
Ben314 a écrit:Tu (on) tourne en rond : comment prouve tu qu'il y a bien trois surfaces, c'est à dire qu'il est impossible d'aller de haut en bas sans couper ?
Le problème n'est pas de définir les chemins, c'est de montrer qu'ils séparent en plusieurs zones.
je ne comprends pas,
tu ne considères pas qu'un seul chemin d'un bord de l'échiquier à l'autre en face fait 2 surfaces?
et donc un deuxième chemin au-dessus ou au-dessous redivise une des deux surfaces encore en deux,
donc deux chemins ne se croisant pas font 3 surfaces.
Ceci n'est pas admis?
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
@fatal_error : j'ai pas totalement lu les détails, mais l'idée de montrer que "toute courbe est infranchissable" par récurrence sur une des deux dimensions du rectangle doit parfaitement fonctionner.
Ben non, pour moi "l'énigme", ben ça consiste trés exactement à démontrer cette propriété : tout chemin de "droite" à "gauche" coupe l'échiquier en au moins deux "surfaces" (mathématiquement je dirait plutôt "composante connexe")beagle a écrit:tu ne considères pas qu'un seul chemin d'un bord de l'échiquier à l'autre en face fait 2 surfaces?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Ben314 a écrit:@fatal_error : j'ai pas totalement lu les détails, mais l'idée de montrer que "toute courbe est infranchissable" par récurrence sur une des deux dimensions du rectangle doit parfaitement fonctionner.
Ben non, pour moi "l'énigme", ben ça consiste trés exactement à démontrer cette propriété : tout chemin de "droite" à "gauche" coupe l'échiquier en au moins deux "surfaces" (mathématiquement je dirait plutôt "composante connexe")
Qu'appelles-tu chemin?
Il y a le chemin enchevétrée du jeu qui n'est pas la notion de chemin de la théorie des graphes il me semble.
Je croyais qu'il fallait démontrer cela pour chemin zarbi de la pièce,
mais que était admis qu'un chemin de la théorie des graphes divisait une surface en deux?
le but de ma démonstration étant de passer de chemin fou du pion à un chemin type chemin de la théorie des graphes.
(si tant est que j'ai bien compris aussi ce que celait recouvrait mais bon)
PS:Peut-ètre que je veux dire chemin élémentaire.
c'est ceux-là qui divisent sans soucis une surface en deux?
ou bien mème ceux-là ne te conviennent pas.
Il n' y a pas des chemins en théorie des graphes qui divisent une surface connexe en deux?
Je pensais que le problème pouvait se résoudre en transformant le chemin complexe en un chemin "élémentaire?" acceptable pour dire OK, cela divise en deux.
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
nodjim a écrit:Ces 2 points sont sur la frontière extérieure (facile à prouver).
Certainement, c'est facile de prouver qu'un truc est sur un truc qu'on a pas défini.
Pour dessiner le contour: on peut, par exemple, à partir d'un de ces points, dessiner, dans le territoire, et sur le bord, un trait continu: on prend un sens arbitraire et on suit toujours le bord main gauche par exemple. Est ce qu'on ne fera pas le tour complet du territoire et est ce qu'on ne reviendra pas au point de départ ?
Bien, alors, je t'accorde le droit de passer sur comment on prolonge la ligne bord par bord, et sur le fait qu'elle finisse par boucler vu qu'on fait tourner un algo qui a un nombre fini d'états.
J'imagine que la frontière a le droit de passer par les bords de l'échiquier.
Quel est exactement ton point de départ ? Tu prends deux cases C1 et C2 les plus "éloignées" du territoire, et tu prends un bord B de C1 qui est encore plus "éloignée" de C2 ?
Comment tu vas faire pour prouver que ce que tu obtiens est indépendant de ton choix de (C1,C2,B) ?
Genre ne serait-ce qu'en échangeant C1 et C2, il est pas du tout évident qu'on va obtenir la même "frontière extérieure".
@fatal_error : si j'ai bien suivi tu as une notion de "courbe qui sépare un rectangle de hauteur h en deux", tu dis que quand h=2 ça marche, puis tu fais une récurrence.
Je crois pas avoir vu de moment où tu expliquais, pendant l'étape de récurrence, comment à partir d'un chemin horizontal dans un rectangle de hauteur (h+1) tentant de traverser le chemin infranchissable, tu obtenais un chemin horizontal dans le sous-rectangle de hauteur h pour pouvoir appliquer l'hypothèse de récurrence. Ou alors tu l'as fait mais j'ai rien compris ?
Bon, ça fait au moins 4 fois que je le dit : un "chemin de la théorie des graphes", ça n'a RIEN A VOIR avec ce qu'on appele un chemin sur une feuille de papier : un graphe, c'est un objet purement algébrique : c'est la donnée de deux types d'objects que l'on appelle "sommets" et "arrêtes" mais les sommets ne sont absolument pas des "points du plan" (ou d'un autre espace) et les arrêtes ne sont absolument pas des courbes continues ou quoi que ce soit d'autre de représentable sur une feuille de papier !!!
Donc, si tu veut, tu peut utiliser la théorie des graphes, mais il faut commencer par préciser quel est l'ensemble des "sommet" et celui des "arrêtes"
Donc, si tu veut, tu peut utiliser la théorie des graphes, mais il faut commencer par préciser quel est l'ensemble des "sommet" et celui des "arrêtes"
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
