Un chemin de tour
40 messages
- Page 1 sur 2 - 1, 2
Un chemin de tour
J'aime particulièrement les problèmes d'apparence simple et dont la solution ( un peu astucieuse ) donne sa chance à chacun .
Sur un échiquier infini , on a marqué 2n cases de telle sorte qu'une tour ( j'espère que tout le monde connait les règles du jeu d'échec ) peut visiter toutes les cases sans empiéter sur l'extérieur : c'est son territoire . Montrer que le territoire d'une tour peut être divisé en n rectangles d'intérieurs disjoints .
Amusez-vous bien ( j'en ai quelques autres en réserve :we: )
Imod
Sur un échiquier infini , on a marqué 2n cases de telle sorte qu'une tour ( j'espère que tout le monde connait les règles du jeu d'échec ) peut visiter toutes les cases sans empiéter sur l'extérieur : c'est son territoire . Montrer que le territoire d'une tour peut être divisé en n rectangles d'intérieurs disjoints .
Amusez-vous bien ( j'en ai quelques autres en réserve :we: )
Imod
En effet mon texte n'est pas clair :--:
Un petit exemple pour illustrer .

Sur le dessin on a un territoire de tour de huit cases ( la tour peut le visiter en entier sans en sortir ) . On a divisé le territoire en quatre rectangles d'intérieurs disjoints .
rectangles d'intérieurs disjoints .
Il faut montrer que c'est toujours possible :we:
Imod
Un petit exemple pour illustrer .

Sur le dessin on a un territoire de tour de huit cases ( la tour peut le visiter en entier sans en sortir ) . On a divisé le territoire en quatre
Il faut montrer que c'est toujours possible :we:
Imod
Imod a écrit:En effet mon texte n'est pas clair :--:
Un petit exemple pour illustrer .
Sur le dessin on a un territoire de tour de huit cases ( la tour peut le visiter en entier sans en sortir ) . On a divisé le territoire en quatrerectangles d'intérieurs disjoints .
Il faut montrer que c'est toujours possible :we:
Imod
Hum, j'avais mal compris :doh: . Dans l'exemple, tu représentes 8 cases jointes, or une tour saute les cases intermédiaires. Je pensais donc que les 2n cases étaient, le plus souvent, non voisines. Et que les rectangles à former groupaient 2 cases, alignées ou pas, parmi les 2n. Du coup, je ne comprends plus.
On peut aussi dire (si j'ai bien compris) qu'il s'agit des cases où une tour peut aller en plusieurs coups si on lui interdit certaines cases. Cela définit un parcours que la tour peut effectuer, qui lui est accessible, en un nombre fini de coups. Le nombre de cases du parcours autorisé à la tour est pair, et on cherche à prouver qu'on peut recouvrir les cases par des rectangles d'intérieur disjoints au nombre de n.
Imod a écrit:
Une tentative de preuve :
Mon but va être de montrer qu'on peut trouver un recouvrement du territoire par des rectangles disjoints qui sont en nombre inférieur à n. En effet, s'il existe un tel recouvrement, alors il suffira de scinder suffisamment de fois les rectangles de ce recouvrement pour parvenir à un nombre n de rectangles disjoints de recouvrement. Toute ma preuve est basée là-dessus.
Comment montrer qu'il existe un recouvrement de taille inférieure à n? (par taille du recouvrement, j'entends nombre de rectangles disjoints du recouvrement, vous l'aurez compris) Pour ce faire j'ai essayé de considérer les rectangles les plus grands possible.
J'introduis la notion de rectangle horizontal maximal ou de rectangle vertical maximal, un rectangle horizontal maximal étant un rectangle horizontal dont la case la plus à droite ainsi que la case la plus à gauche n'ont pas de case horizontalement adjacente (adjacente sur la même ligne) respectivement à droite et à gauche. Idem pour un rectangle maximal vertical.
Mon idée de départ était celle-ci : si je trouve un recouvrement par des rectangles tous de taille au moins 2, alors il y en aura au plus 2n/2 = n. Malheureusement, il existe des cas où un tel recouvrement est impossible, par exemple (je dessine des ronds au lieu de rectangles, je ne pense pas que ça gêne la compréhension) :
OOO
- O
Le problème vient des cases qui restent seules, qui dépassent.
Cela a guidé cette méthode :
Je colorie tous les rectangles horizontaux maximaux de longueur exactement 2, qui sont au nombre de k. Puis je colorie tous les rectangles verticaux maximaux de longueur exactement 2 - au nombre de p - parmi les cases non coloriées restantes.
Les seuls cases restantes sont donc soit des cases représentant un rectangle maximal à elles toutes seules (en tenant compte du fait qu'on ne prend plus en compte les cases coloriées) soit des cases faisant partie d'un rectangle maximal de longueur plus grande ou égale à 3 : autrement dit les seuls rectangles maximaux qui restent sont soit des cases, soit des rectangles de longueur supérieure ou égale à 3 : on les colorie également.
La seule chose qui pose problème maintenant, ce ne sont ni les rectangles de longueur 2, ni ceux de longueur 3 ou plus, mais ceux de longueur 1, qui sont les seuls à rester non coloriés. De quelle nature sont-ils?
Puisqu'on a commencé par colorier les k rectangles horizontaux maximaux de longueur exactement 2, il n'y a aucune case qui dépasse horizontalement, c'est à dire qu'une case telle que la case tout à droite dans l'exemple ci-dessous
O
OO
O
est forcément déjà coloriée car soit elle n'a à sa gauche qu'une seule case, osoit elle fait partie des rectangles horizontaux maximaux de longueur au moins 3 (si on est dans ce cas :
-O
OOO
-O
)
Par conséquent les seules cases susceptibles de rester non coloriées sont les cases correspondant à une des deux cases de rectangles verticaux maximaux (qui sont tels avant que toute coloration n'ait été effectuée) de longueur 2, ce qui correspond par exemple à la case tout en haut dans l'exemple ci-dessous :
O
OO -> ont été coloriées lors du 1er coloriage
-OOOOO -> ont été coloriées lors du 3ème coloriage
On voit qu'ils ne peuvent apparaître que greffés à des rectangles horizontaux maximaux de longueur 2.
A partir de ça on va essayer de majorer le nombre de rectangles de longueur au moins égale à 3.
Il y en a au plus
(2n - 2k - 2p)/3 = (2/3)n - 2/3 (k+p).
Notons s le nombre de ces cases solitaires,
alors le nombre total de rectangles est au plus de
(2/3)n - 2/3 (k+p -s) + k + p s= (2/3)n + (1/3) k + (1/3)p + (1/3)s
Or p< n-k-s
donc
le nombre total de rectangles est plus petit que n.
D'après l'assertion au tout début de mon post, ceci prouve qu'il existe une partition de n rectangles d'intérieurs disjoints de l'ensemble du territoire.
J'espère qu'il n'y a pas d'erreur et que vous m'avez compris. Il y a sans doute plus simple (j'ai essayé avec des applications mais je n'ai rien trouvé) mais bon, en tout cas je me suis bien amusé.
Je pense qu'au lieu de prendre les rectangles horizontaux maximaux de taille 2, il faut que je prenne des rectangles d'une taille égale à celle du plus petit rectangle horizontal maximal de taille au moins égale à 2.
Dans ton exemple, cela donne pour commencer la ligne de 3 cases. Ensuite je fais pareil avec les rectangles verticaux : je colorie le plus petit rectangle maximal parmi ceux de taille au moins 2, c'est-à-dire celui du bas. Reste enfin celui du haut.
Soit h la taille minimale des rectangle horizontaux maximaux, et v la taille minimale des rectangles verticaux maximaux.
Soit m = min (h,v).
Soit k le nombre de rectangles horizontaux maximaux de taille h, p le nombre de rectangles verticaux maximaux de taille v restant une fois qu'on a enlevé les k derniers.
Alors il y a moins de
(2n - (h+1)k - (v+1)p) / (m+1)
rectangles de taille au moins m+1.
Il y a ensuite k rectangles de taille h, p rectangles de taille v, et s rectangles solitaires.
Cela fait donc moins de :
(2n - (h+1)k - (v+1)p) / (m+1) + k + p + s
rectangles formant un recouvrement, ie
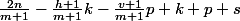
}{m+1})
donc il y a moins de
}{m+1})
rectangles,
Supposons que par exemple h = min(h,v) = m, alors la quantité précédente est inférieure à :
 + \frac{v-m}{m+1}p + \frac{s(v+1)}{m+1})
Or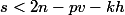
d'où (après calculs que je vous laisse vérifier à la main, et en utilisant le fait que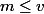 ) :
) :
la quantité précédente est inférieure à :
 + 4n}{m+1})
Quel est le maximum de + 4n) en fonction de n et p?
en fonction de n et p?
Les calculs donnent :
 = f(p)) ,
,
cherchons-en le maximum en fonction de p en gardant à l'esprit que p<n :
 = -3p^{2} - 4p + 4n + 4pn - 4n^{2} = -3p^{2} + p(4n-2) + 4n - 4n^{2})
Les calculs donnent que le maximum de cette fonction est atteint pour p = (2n-1)/3...
et là j'ai plus la force de calculer le maximum... Je pense que ça a de grandes chances de pas aboutir vu comme c'est parti... Bon au moins j'aurais essayé. J'essaierai de reprendre les calculs quand j'aurais le temps.
A tous les coups il y a beaucoup plus simple, mais je n'ai pas trouvé en essayant d'autres raisonnements.
Dans ton exemple, cela donne pour commencer la ligne de 3 cases. Ensuite je fais pareil avec les rectangles verticaux : je colorie le plus petit rectangle maximal parmi ceux de taille au moins 2, c'est-à-dire celui du bas. Reste enfin celui du haut.
Soit h la taille minimale des rectangle horizontaux maximaux, et v la taille minimale des rectangles verticaux maximaux.
Soit m = min (h,v).
Soit k le nombre de rectangles horizontaux maximaux de taille h, p le nombre de rectangles verticaux maximaux de taille v restant une fois qu'on a enlevé les k derniers.
Alors il y a moins de
(2n - (h+1)k - (v+1)p) / (m+1)
rectangles de taille au moins m+1.
Il y a ensuite k rectangles de taille h, p rectangles de taille v, et s rectangles solitaires.
Cela fait donc moins de :
(2n - (h+1)k - (v+1)p) / (m+1) + k + p + s
rectangles formant un recouvrement, ie
donc il y a moins de
rectangles,
Supposons que par exemple h = min(h,v) = m, alors la quantité précédente est inférieure à :
Or
d'où (après calculs que je vous laisse vérifier à la main, et en utilisant le fait que
la quantité précédente est inférieure à :
Quel est le maximum de
Les calculs donnent :
cherchons-en le maximum en fonction de p en gardant à l'esprit que p<n :
Les calculs donnent que le maximum de cette fonction est atteint pour p = (2n-1)/3...
et là j'ai plus la force de calculer le maximum... Je pense que ça a de grandes chances de pas aboutir vu comme c'est parti... Bon au moins j'aurais essayé. J'essaierai de reprendre les calculs quand j'aurais le temps.
A tous les coups il y a beaucoup plus simple, mais je n'ai pas trouvé en essayant d'autres raisonnements.
Imod a écrit:Je crains que ta nouvelle stratégie échoue encore dans le cas ci-dessous :marteau:
Imod
Ma stratégie n'aboutit pas à une démonstration, pas encore en tout cas, cependant elle traite le cas que tu indiques : d'abord elle colorie la première ligne, ensuite elle colorie les cases solitaires (il y a 0 rectangle vertical maximal).
Alors je ne dois pas avoir compris ta stratégie :doh:
Le territoire est l'ensemble des cases jaunes et rouges ( voir mon dessin ) .
Ce que j'ai cru comprendre :
1°) Tu repères le plus petit rectangle maximal horizontal de taille supérieure ou égale à deux . Ici il y en a qu'un : le rectangle jaune .
2°) Il ne reste alors que quatre cases isolées ce qui donne cinq rectangles en tout : un de trop :marteau:
Imod
Le territoire est l'ensemble des cases jaunes et rouges ( voir mon dessin ) .
Ce que j'ai cru comprendre :
1°) Tu repères le plus petit rectangle maximal horizontal de taille supérieure ou égale à deux . Ici il y en a qu'un : le rectangle jaune .
2°) Il ne reste alors que quatre cases isolées ce qui donne cinq rectangles en tout : un de trop :marteau:
Imod
Alpha a écrit:Effectivement, bien que ce cas soit traité par ma stratégie, ma stratégie aboutit à un nombre de rectangles non optimal. Il faut donc que je revoie ma stratégie, et même très certainement que je laisse tomber mon approche.
Ton approche n'est pas mauvaise en tout cas pas complètement , la bonne idée est bien de repérer les rectangles maximaux horizontaux et verticaux . La partition en rectangle est alors "simplissime" , il "suffit" de la voir et montrer qu'elle convient .
Ce problème issue du tournoi des villes n'est pas simple ce qui rend encore plus jolie la solution , courte et limpide :we:
Imod
40 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 6 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

