Un cercle dans un triangle

par **Imod** » 07 Oct 2007, 19:05

Le site Regina nous a offert il y a quelque temps un mémorable problème de pièces de monnaie ( certains s'en souviennent sûrement ) . Celui d'octobre 2007 est intéressant car abordable par un élève de seconde . A vous les lycéens !!!

Un cercle de centre O et de rayon 1 cm roule à l'intérieur d'un triangle dont les côtés mesurent 6,8 et 10 cm respectivement , en longeant les côtés . Quelle distance O parcourt-il en un circuit complet ?

Imod

par **FlyGhost** » 09 Oct 2007, 18:08

En tattonant, je fait Thales avec un facteur 1/2 et je trouve ke O parcours 3+4+5=12 cm. Mais bon lol pas super precis comme methode

par **Imod** » 09 Oct 2007, 19:07

C'est un peu plus compliqué :we:

Imod

Edit : mais d'accord sur le résultat .

par **alben** » 10 Oct 2007, 12:31

Imod a écrit: mais d'accord sur le résultat .

Curieux, de mémoire, ce n'est pas ce que j'avais trouvé. C'était bien plus :doh:

PS Au temps pour ma mémoire, c'était bien ça

par **Imod** » 10 Oct 2007, 18:20

Une généralisation amusante et curieusement à peine plus difficile . Le triangle est quelconque de côtés a,b et c , un cercle de rayon r suit intérieurement les côtés du triangle , quelle distance a parcouru son centre quand il a fait un tour complet ?

Imod

par **nuage** » 10 Oct 2007, 21:11

Salut,
je trouve :

en supposant

sinon le cercle ne rentre pas dans le triangle.
La formule est compliqué, et j'espère ne pas avoir fait d'erreur en la tapant, mais il est vrai que le raisonnement géométrique est simple.

Pour ceux qui veulent le chercher, un indice en blanc :
penser au cercle inscrit dans le triangle (et à son centre)

par **Imod** » 10 Oct 2007, 22:23

nuage a écrit:je trouve :

Une belle formule qui s'exprime quand même plus simplement à l'aide du périmètre et de l'aire du triangle ( mais moi aussi j'aime bien jouer à LaTeX :we: ) .

Imod

par **nuage** » 13 Oct 2007, 22:48

Salut,

Imod a écrit:Une belle formule qui s'exprime quand même plus simplement à l'aide du périmètre et de l'aire du triangle ( mais moi aussi j'aime bien jouer à LaTeX :we: ) .

Imod

à l'aide du rayon du cercle inscrit dans le triangle c'est encore plus simple.
Mais ton observation est juste : je m'entraine à

.
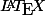
mais je n'ai pas encore vraiment sauté le pas.

par **aviateurpilot** » 13 Oct 2007, 23:07

O dessine un triangle semblable au grand triangle
donc on a qu'a calcule la distance

qu'a parcouru O sur le segment (6cm)
et donc ce cas la solution est

est facile a touvé.

par **Imod** » 13 Oct 2007, 23:16

aviateurpilot a écrit:
est facile a trouver.

Comment ?

Imod

par **nuage** » 13 Oct 2007, 23:17

Salut aviateurpilot je ne comprend pas ta solution.
Peux tu l'expliciter.

Un cercle dans un triangle

Un cercle dans un triangle

Qui est en ligne