Calotte sphérique "optimale"

[methusalah]

Bonjour à tous,

Pour un projet architectural, je cherche à déterminer la hauteur d'une calotte sphérique qui possède le meilleurs rapport entre son volume (le plus grand) et sa surface sphérique, base comprise (la plus petite)

Pour le moment, par tâtonnement, je n'ai rien trouvé de mieux que la demi sphère, soit h=R. Cela dit je n'ai pas réussi à pondre une équation fiable.

Quelqu'un peut il aider ?

Merci d'avance !

[Ben314]

Salut,
Exprimé de cette façon, le problème n'a pas de solution : Si on fait une homothétie de rapport , le volume est multiplié par et la surface par 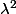donc le rapport Volume/Surface est multiplié par et peut être rendu aussi grand que l'on veut.

Donc si on veut que le problème soit intéressant, il faut plutôt le formuler sous la forme :
"Pour une surface donnée, quel est le plus grand volume que l'on peut obtenir"
ou bien sous la forme
"Pour un volume donné, quelle est la plus petite surface possible"

A mon avis c'était bien ça le sens de ta question et... je vais regarder...

[Ben314]

Je viens de faire les calculs et je tombe sur un résultat qui est en fait... évident...
En fait, on sait que, pour une surface donnée, la "forme" qui a le plus grand volume est la sphère.
Et, comme la sphère complète fait partie des solutions acceptables de ton problème (lorsqu'on le modélise avec une hauteur de coupe ) c'est évidement elle qui donnera le plus grand volume...
Sauf erreur, cela signifie que, si on limite le problème à , le max sera forcément "au bord" du domaine d'étude, c'est à dire pour h=R.

[methusalah]

Merci pour la recherche. Effectivement le résultat semble tomber sous le sens, et effectivement la question était mal posée en soit. Le volume et la surface croissent proportionnellement donc la réponse ne peux être que l'extrême.

Cela dit, as tu considérer l'ajout de surface du plan de coupe (la "base" de la coupole) dans tes calculs ? Je doute que ça change quelque chose mais je préfère vérifier.

Sache que mon intervalle pour la hauteur est de 0 à R, c'est à dire une demi sphère max.

Merci encore pour ton temps