Exprimer en fonction de n la somme:
Calculer une somme
11 messages
- Page 1 sur 1
Bonjour Chan,
Ma proposition (pour rigoler)
Ma proposition (pour rigoler)
- Code: Tout sélectionner
#include
#include
#include
int main()
{
printf("Calcul d'une somme (somme de 0 à n de k au cube divisé par 2 puissance k n=?\n");
char Ligne[40];
int n;
gets(Ligne);
sscanf(Ligne, "%d",&n);
unsigned int Somme=0;
if (n > 0)
{
for (int i=0; i<=n; i++)
{
Somme = Somme + (int)(i*i*i / pow(2.0, (double)i) );
}
}
printf("le résultat est %d\n",Somme);
getch();
return 0;
}
Salut Chan,
U0=0
Un=3/2 +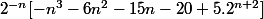 je n'ai pas trop vérifié, il y a certainement des erreurs de calculs mais pour n=1 et n=2 cela coïncide c'est miraculeux si je ne me suis pas loupé :zen:
je n'ai pas trop vérifié, il y a certainement des erreurs de calculs mais pour n=1 et n=2 cela coïncide c'est miraculeux si je ne me suis pas loupé :zen:
( bon je l'avoue, j'ai triché pour les dérivées seconde et troisième, cela devenait trop pénible :ruse:) Tu as une autre méthode?
U0=0
Un=3/2 +
( bon je l'avoue, j'ai triché pour les dérivées seconde et troisième, cela devenait trop pénible :ruse:) Tu as une autre méthode?
jlb a écrit:salut Chan, où as-tu trouvé cette question, cela a une application pratique? Bon, j'ai trouvé une méthode avec pas mal de calculs ( à l'aide d'une série et de ses dérivées). Y a-t-il une autre méthode? Merci. [Par contre, Wolfram donne immédiatement rapidement la solution ]
J'avais été amené à calculer
et du coup, j'ai essayé de voir ce que ça donnait avec
On peut peut-être généraliser, je n'ai pas essayé.
chan79 a écrit:J'avais été amené à calculer
et du coup, j'ai essayé de voir ce que ça donnait avec
On peut peut-être généraliser, je n'ai pas essayé.
Salut, on peut généraliser la méthode de jlb à n'importe quelle somme du type
L'idée est de remarquer que si on pose
En exprimant k^p comme combinaison linéaire des
Genre pour p = 3, la somme vaut
En fait si on exprime ^px^k) avec le binôme de Newton, et d'une autre manière en changeant d'indice, on peut obtenir une relation de récurrence. Sauf erreur de ma part :
avec le binôme de Newton, et d'une autre manière en changeant d'indice, on peut obtenir une relation de récurrence. Sauf erreur de ma part :
=\frac{(n+1)^{p+1}x^{n+1}}{x-1}+\frac{x}{1-x}\sum_{j=0}^p \begin{pmatrix}p+1 \\ j\end{pmatrix}S_{n,j}(x))
avec=\sum_{k=0}^n k^px^k) . Du coup si x est donné numériquement on peut calculer les sommes de proche en proche sans avoir à passer par le calcul fastidieux des dérivées.
. Du coup si x est donné numériquement on peut calculer les sommes de proche en proche sans avoir à passer par le calcul fastidieux des dérivées.
avec
Skullkid a écrit:Salut, on peut généraliser la méthode de jlb à n'importe quelle somme du typeavec p entier naturel et x réel (différent de 1, sinon on est ramené au problème plus simple des sommes de puissances d'entiers consécutifs). Si x et p sont donnés numériquement et que p est grand, il faut avoir pas mal de temps libre (ou un programme dédié) pour obtenir la formule en fonction de n...
L'idée est de remarquer que si on pose, alors la dérivée m-ième de f_n est
.
En exprimant k^p comme combinaison linéaire des, pour m entre 0 et p, on obtient quelque chose du genre
, où les a_m,p sont les coefficients de la combinaison linéaire.
Genre pour p = 3, la somme vaut(qui est déjà une expression plutôt lourde si on ne donne pas de valeur numérique à x). Je ne pense pas qu'il soit possible de donner une formule générale explicite en fonction de n, x et p, mais on doit pouvoir prouver des trucs sur la forme du résultat, genre un polynôme en n et x de degrés p en n et n+p en x, divisé par (1-x)^(p+1)...
Ok et merci pour tout ça.
J'avais fait simplement ceci:
D'abord
La première somme est téléscopique et la seconde est simple à calculer. On arrive à :
Ensuite
On a encore une somme téléscopique et on utilise le résultat précédent.
On obtient
Et enfin, de la même façon avec
on arrive au résultat demandé :
Au passage, on voit que la limite est 26
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
