Vu que j'ai posté un autre truc sur le fil d'à côté alors autant laisser tomber celui-là en donnant tout de suite la solution (oui je ne peux pas dire que je le laisse tomber tant qu'il n'est pas terminé)
bah voilà comme ça c'est expédié
Solution de
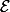Notations au préalable :
Première notation:
)
ensemble des matrices à
lignes et
colonnes à coefficients dans
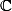
Deuxième notation:
)
ensemble des matrices non nulles à
lignes et
colonnes à coefficients dans
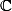
Troisième notation:
)
ensemble des matrices carrées de taille
à coefficients dans
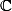
Quatrième notation:
)
ensemble des matrices carrées et non nulles de taille
à coefficients dans
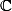
Cinquième notation:
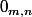
la matrice nulle de
Sixième notation:
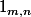
la matrice de
dont le coefficient situé à la
-ième ligne et
-ième colonne est de valeur
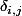
avec le symbole de Kronecker
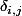
selon
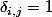
si
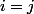
et
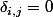
sinon
Septième notation:
)
ensemble des matrices inversibles de taille
à coefficients dans
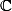
Huitième notation:
Pour une matrice
)
on propose la notation
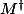
qui désigne la matrice adjointe
(i.e. la matrice transconjuguée) de
Neuvième notation:
Pour une matrice
on propose la notation
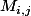
qui désigne le coefficient de
situé à la
-ième ligne et
-ième colonne
______________
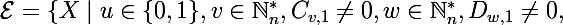
,A^{ \dagger }M^{-1}\left(M^{ \dagger }\right)^{-1}B\in \mathcal {M}_{1}^*\left(\mathbb {C}\right),V\in \mathcal {M}_{n,1}\left(\mathbb {C}\right),W\in \mathcal {M}_{n,1}\left(\mathbb {C}\right)\})
Première remarque: Une solution triviale pour
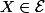
existe lorsque
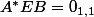
c'est évidemment la matrice carrée nulle
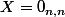
L'ensemble proposé prend en compte cette solution évidemment comme on peut s'en rendre compte dans la description de la définition de
(voir la septième remarque en fin de propos)
Pour définir
on va poser
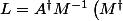^{-1}B)
et
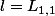
Deuxième remarque: Il est stipulé que
est choisi de telle sorte que
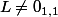
par conséquent on doit avoir
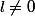
Puis on pose
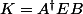
et
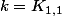
et
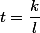
Lorsque
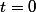
on pose
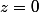
sinon on pose:
Lorsque
\geq 0)
on pose
}{\left|\left|t\right|\right|}\right))
sinon on pose
}{\left|\left|t\right|\right|}\right))
Troisième remarque: Lorsque
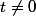
alors
est l'argument principal de
dans
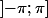
Lorsque
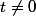
on pose
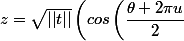+i.sin\left(\dfrac {\theta +2\pi u}{2}\right)\right))
Quatrième remarque:
est une racine de
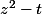
Puis on pose
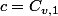
et
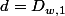
Cinquième remarque: Il est stipulé que
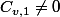
et
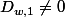
de sorte que
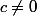
et
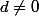
À présent on va considérer une application
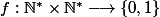
\mapsto \left\lfloor \dfrac {2\left\lfloor \dfrac {x}{y}\right\rfloor}{\left\lfloor \dfrac {x}{y}\right\rfloor +1}\right\rfloor)
Sixième remarque: Avec cette application on vérifie
=1)
ssi
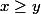
et
=0)
sinon
Puis on pose
f\left(i,v\right)-1\right)\overline {C}_{i,1}V_{i,1}}{\overline {c}})
f\left(i,w\right)-1\right)\overline {W}_{i,1}D_{i,1}}{d})
Enfin on va considérer les matrices
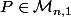
et
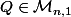
dont les coefficients
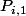
et
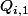
sont définis par
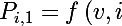f\left(i,v\right)p+\left(1-f\left(v,i\right)f\left(i,v\right)\right)V_{i,1})
f\left(i,w\right)\overline {q}+\left(1-f\left(w,i\right)f\left(i,w\right)\right)W_{i,1})
Alors
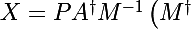^{-1}BQ^{ \dagger })
septième remarque: Lorsque
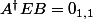
la solution triviale
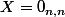
est obtenue en posant
,
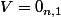
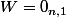
et on remarque que cette matrice nulle
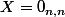
n'est jamais obtenue quand
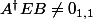
et même si
,
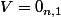
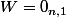
Sujet clos (inutile de faire la deuxième question avec la solution pour
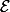
pas la peine de s'emmerder autant écrire un petit programme sur sa machine et basta elle le fera elle-même et elle l'affichera sur l'écran elle-même)
