Bonne inéqualité!
Olympiades mathématiques, énigmes et défis
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 03 Déc 2006, 12:45
par darkmaster » 03 Déc 2006, 12:45
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 03 Déc 2006, 13:43
par darkmaster » 03 Déc 2006, 13:43
aviateurpilot a écrit:soit
=\frac{\sqrt{x}}{1-x})
on a
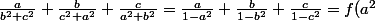+f(b^2)+f(c^2)\ge 3f(\frac{a^2+b^2+c^2}{3})=3\frac{\sqrt{1/3}}{1-\frac{1}{3}}=3\frac{\sqrt{3}}{2})
Tu as appliqué Jensen inégalité.
Tu es sûr que
)
est toujours positive avec
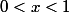
?
Moi, je crois que non.
Si

,
<0)
.

-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 03 Déc 2006, 14:08
par aviateurpilot » 03 Déc 2006, 14:08
dsl,
mais j'ai meme pas verifie que f" est tjrs positif sur ]0,1[
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 18 Déc 2006, 19:10
par Imod » 18 Déc 2006, 19:10
Je n'avais pas encore essayé car je ne suis jamais très à l'aise avec les inégalités mais celle-ci est simple ( aviateurpilot n'était pas loin ) .
On pose
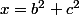
,
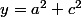
,
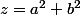
et
=\frac{\sqrt{1-t}}{t})
pour
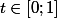
. Alors f est positive , décroissante , convexe sur

et
=\frac{\sqrt{3}}{2})
.
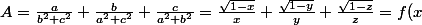+f(y)+f(z))
.
on a :
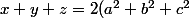=2)
et comme

est convexe :
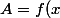+f(y)+f(z)\geq3f(\frac{x+y+z}{3})\geq 3f(\frac{2}{3})=\frac{3\sqrt{3}}{2})
Imod
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 19 Déc 2006, 11:32
par darkmaster » 19 Déc 2006, 11:32
Imod a écrit:Je n'avais pas encore essayé car je ne suis jamais très à l'aise avec les inégalités mais celle-ci est simple ( aviateurpilot n'était pas loin ) .
On pose
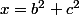
,
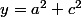
,
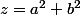
et
=\frac{\sqrt{1-t}}{t})
pour
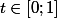
. Alors f est positive , décroissante , convexe sur

et
=\frac{\sqrt{3}}{2})
.
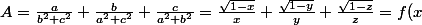+f(y)+f(z))
.
on a :
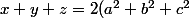=2)
et comme

est convexe :
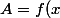+f(y)+f(z)\geq3f(\frac{x+y+z}{3})\geq 3f(\frac{2}{3})=\frac{3\sqrt{3}}{2})
Imod
f n'est pas convexe sur

:zen:
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 19 Déc 2006, 16:42
par Imod » 19 Déc 2006, 16:42
darkmaster a écrit:f n'est pas convexe sur

:zen:
Tiens c'est vrai ( j'avais un peu raté ma dérivée seconde ) :briques: . Il reste donc à voir ce qui se passe si deux des valeurs sont inférieures à la borne fatidique et une supérieure .
Imod
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 19 Déc 2006, 21:34
par darkmaster » 19 Déc 2006, 21:34
Moi, Je ne pense pas que Jensen soit une bonne idée pour ce problème...
:triste:
 par sandrine_guillerme » 19 Déc 2006, 22:05
par sandrine_guillerme » 19 Déc 2006, 22:05
Salut
C'est un problème d'olympiade très classique
je crois que j'ai la réponse mais je sais plus ou est t elle si vous voulez je la cherche pour vous ?
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 19 Déc 2006, 23:06
par darkmaster » 19 Déc 2006, 23:06
Oui, il est très classique et la solution est très belle.Mais pourquoi la chercher? On peut la trouver car elle est pas compliquée du tout.
J'ai cette solution, si personne ne peut la trouve, je vais la poster.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 19 Déc 2006, 23:46
par Imod » 19 Déc 2006, 23:46
darkmaster a écrit:Oui, il est très classique et la solution est très belle.Mais pourquoi la chercher? On peut la trouver car elle est pas compliquée du tout.
J'ai cette solution, si personne ne peut la trouve, je vais la poster.
Un bon problème d'olympiade est toujours astucieux et dire qu'il n'est pas compliqué ne veut pas dire grand chose , l'outil employé est sans doute simple mais la bonne idée de son utilisation ne l'est sûrement pas . Le fait de détenir depuis un moment la réponse au problème donne une fausse impression de facilité , je connais des exercices de niveau collège ou même primaire sur lesquels j'ai séché ( sans honte ) un bon moment !!!
Imod
PS : Laisse-moi chercher encore un peu .
PPS : Si tu pouvais corriger l'erreur dans la formule initiale ! merci d'avance .
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 20 Déc 2006, 00:12
par darkmaster » 20 Déc 2006, 00:12
Je l'ai corrigée, merci.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 23 Déc 2006, 18:54
par Imod » 23 Déc 2006, 18:54
Je crois que j'ai trouvé l'astuce :id:
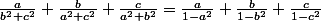
En étudiant les variations de
=x-x^3)
sur [0;1] on constate qu'elle atteint son maximum en
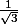
et que ce maximum est

donc par exemple :

donc
})
et

. On obtient des inégalités similaires avec b et c et en ajoutant les trois

Imod
-
yos
- Membre Transcendant
- Messages: 4858
- Enregistré le: 10 Nov 2005, 20:20
-
 par yos » 24 Déc 2006, 00:39
par yos » 24 Déc 2006, 00:39
Ca semble tout simple vu comme ça. Bravo.
-
darkmaster
- Membre Naturel
- Messages: 74
- Enregistré le: 18 Oct 2006, 22:40
-
 par darkmaster » 24 Déc 2006, 00:51
par darkmaster » 24 Déc 2006, 00:51
Bravo, Imod. c'est bien ça.
La clé du problème est

. Tu l'as bien trouvée.
On peut la démontrer par une méthode d'olympiade. Elle équivaut à
^3 \geq 3\sqrt{3}a)
qui est absolument vrai car
^3 \geq 3\sqrt[3]{1.1.(\sqrt{3}a)^3} = 3\sqrt{3}a)
Merci pour ta solution.
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 24 Déc 2006, 00:59
par Imod » 24 Déc 2006, 00:59
Tout simple ! j'ai quand même rempli des pages de calcul pour arriver au résultat , je ne suis pas plus malin que bien d'autres mais particulièrement coriace :hum:
Merci quand même pour les compliments :we:
Imod
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
