Bonsoir
"Vous laurez certainement remarqué, aujourdhui Google a modifié son logo
afin de célébrer la journée de Pi. En effet, le 14 mars écrit au format de date américain (3/14) peut être assimilé à lapproximation de Pi à 3 chiffres : 3,14"
Juste un clin d'il : comment s'orthographierait Ben314 en base 12 ?
Pour les fous furieux.. : qui me donnerait le plus grand nombre de décimales de Pi en base 12 ?
1) en passant par la base 10
2)En supposant ne connaitre que la base 12!!!! ( ca donne le vertige ?)
Bonne fête BenPi
8 messages
- Page 1 sur 1
Bonne fête Ben318
Je ne résiste pas au plaisir de vous présenter l'algorithme 'compte-goutte'
Calcul de PI en base X 'sans connaitre PI en base 10)
(J'utilise 3,141 ci-dessous pour illustrer mais on ne s'en sert évidemment pas dans le calcul final..)
On va utiliser une (des nombreuses) expression de PI donnée par Euler

ce qui donne :
PI =)))
à rapprocher de la base 10 ou l'on a :
PI =)))
C'est à dire que
PI s'écrit 3,1,4,1 dans la base ' 10' (1, 1/10, 1/10, 1/10, ...)
et
PI s'écrit 2,2,2,2 dans la base 'Euler' : (1, 1/3, 2/5, 3/7, ...)
Ça c'est de la base ! que des 2 pour écrire PI !
Et donc on voit venir la méthode on écrit PI en base Euler PI = 2,22222.... et on ramène dans la base de destination! ! !
on part de PI égal (2,2,2,2,2,2,2,2,2,2,2,2,2,2 ...)
et on commence à calculer 12 *PI
ce qui donne (24,24,24,24,24,24,24,24,24,24,24,24,24,24 ...)
Évidemment il faut faire remonter les 'retenues'
exemple 24 en base 11/23 doit être calculé
comme (1+23) *(11/23)
soit 11 + 1 *( 11/23)
soit 1 avec une retenue de 11
Une fois remontées toute les retenues le nombre de gauche (36) permet de calculer en divisant par 12 le premier chiffre de PI : 3
On enchaine ensuite sur le calcul de la 1° decimale de ( 12 PI -12*3) que l'on trouve en multipliant par 12.....
Et tout ça se fait à la main très aisément, ci dessous le calcul en partant de PI écrit avec 12 décimales 2 :

Les calculs sont menés en base 10, c'est plus facile à suivre
et donc PI = 3,184 en base 12...
Calcul de PI en base X 'sans connaitre PI en base 10)
(J'utilise 3,141 ci-dessous pour illustrer mais on ne s'en sert évidemment pas dans le calcul final..)
On va utiliser une (des nombreuses) expression de PI donnée par Euler
ce qui donne :
PI =
à rapprocher de la base 10 ou l'on a :
PI =
C'est à dire que
PI s'écrit 3,1,4,1 dans la base ' 10' (1, 1/10, 1/10, 1/10, ...)
et
PI s'écrit 2,2,2,2 dans la base 'Euler' : (1, 1/3, 2/5, 3/7, ...)
Ça c'est de la base ! que des 2 pour écrire PI !
Et donc on voit venir la méthode on écrit PI en base Euler PI = 2,22222.... et on ramène dans la base de destination! ! !
on part de PI égal (2,2,2,2,2,2,2,2,2,2,2,2,2,2 ...)
et on commence à calculer 12 *PI
ce qui donne (24,24,24,24,24,24,24,24,24,24,24,24,24,24 ...)
Évidemment il faut faire remonter les 'retenues'
exemple 24 en base 11/23 doit être calculé
comme (1+23) *(11/23)
soit 11 + 1 *( 11/23)
soit 1 avec une retenue de 11
Une fois remontées toute les retenues le nombre de gauche (36) permet de calculer en divisant par 12 le premier chiffre de PI : 3
On enchaine ensuite sur le calcul de la 1° decimale de ( 12 PI -12*3) que l'on trouve en multipliant par 12.....
Et tout ça se fait à la main très aisément, ci dessous le calcul en partant de PI écrit avec 12 décimales 2 :

Les calculs sont menés en base 10, c'est plus facile à suivre
et donc PI = 3,184 en base 12...
LeJeu a écrit:
et donc PI = 3,184 en base 12...
Et en base 10 ça ce marche aussi ?
Ben oui ..

Et oui et comme on peut le voir, c'est facile à mettre en uvre, à programmer ! ( pas de calcul sur de grands nombres, encombrement mémoire raisonnable) la convergence n'est pas révolutionnaire mais franchement honnête !
Je vous donne ci-dessous un petit programme en code C redoutable
[FONT=Courier New]
#include
#include
long a=10000,b,c=8400,d,e,f[8401],g;
void main()
{
for(;b-c;)f[b++]=a/5;
for(;d=0,g=c*2;c-=14,printf("%.4d",e+d/a),e=d%a)
for(b=c; d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);
}[/FONT]
Celui qui l'a écrit dominait en analyse numérique; on sortie , on trouve 2400 décimales de PI :
3,141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233 786 783 165 271 201 909 145 648 566 923 460 348 610 454 326 648 213 393 607 260 249 141 273 724 587 006 606 315 588 174 881 520 920 962 829 254 091 715 364 367 892 590 360 011 330 530 548 820 466 521 384 146 951 941 511 609 433 057 270 365 759 591 953 092 186 117 381 932 611 793 105 118 548 074 462 379 962 749 567 351 885 752 724 891 227 938 183 011 949 129 833 673 362 440 656 643 086 021 394 946 395 224 737 190 702 179 860 943 702 770 539 217 176 293 176 752 384 674 818 467 669 405 132 000 568 127 145 263 560 827 785 771 342 757 789 609 173 637 178 721 468 440 901 224 953 430 146 549 585 371 050 792 279 689 258 923 542 019 956 112 129 021 960 864 034 418 159 813 629 774 771 309 960 518 707 211 349 999 998 372 978 049 951 059 731 732 816 096 318 595 024 459 455 346 908 302 642 522 308 253 344 685 035 261 931 188 171 010 003 137 838 752 886 587 533 208 381 420 617 177 669 147 303 598 253 490 428 755 468 731 159 562 863 882 353 787 593 751 957 781 857 780 532 171 226 806 613 001 927 876 611 195 909 216 420 198 938 095 257 201 065 485 863 278 865 936 153 381 827 968 230 301 952 035 301 852 968 995 773 622 599 413 891 249 721 775 283 479 131 515 574 857 242 454 150 695 950 829 533 116 861 727 855 889 075 098 381 754 637 464 939 319 255 060 400 927 701 671 139 009 848 824 012 858 361 603 563 707 660 104 710 181 942 955 596 198 946 767 837 449 448 255 379 774 726 847 104 047 534 646 208 046 684 259 069 491 293 313 677 028 989 152 104 752 162 056 966 024 058 038 150 193 511 253 382 430 035 587 640 247 496 473 263 914 199 272 604 269 922 796 782 354 781 636 009 341 721 641 219 924 586 315 030 286 182 974 555 706 749 838 505 494 588 586 926 995 690 927 210 797 509 302 955 321 165 344 987 202 755 960 236 480 665 499 119 881 834 797 753 566 369 807 426 542 527 862 551 818 417 574 672 890 977 772 793 800 081 647 060 016 145 249 192 173 217 214 772 350 141 441 973 568 548 161 361 157 352 552 133 475 741 849 468 438 523 323 907 394 143 334 547 762 416 862 518 983 569 485 562 099 219 222 184 272 550 254 256 887 671 790 494 601 653 466 804 988 627 232 791 786 085 784 383 827 967 976 681 454 100 953 883 786 360 950 680 064 225 125 205 117 392 984 896 084 128 488 626 945 604 241 965 285 022 210 661 186 306 744 278 622 039 194 945 047 123 713 786 960 956 364 371 917 287 467 764 657 573 962 413 890 865 832 645 995 813 390 478 027 590 099 465 764 078 951 269 468 398 352 595 709 825 822 620 522 489 407 726 719 478 268 482 601 476 990 902 640 136 394 437 455 305 068 203 496 252 451 749 399 651 431 429 809 190 659 250 937 221 696 461 515 709 858 387 410 597 885 959 772 975 498 930 161 753 928 468 138 268 683 868 942 774 155 991 855 925 245 953 959 431 049 972 524 680 845 987 273 644 695 848 653 836 736 222 626 099 124 608 051 243 884 390 451 244 136 549 762 780 797 715 691 435 997 700 129 616 089 441 694 868 555 848 406 353 422 072 225 828 488 648 158 456 028 50
Merci LeJeu, très intéressant !
En fait, le programme C que tu exhibes applique l'algorithme en base 10000, ce qui lui permet d'afficher quatre chiffres à la fois.
Je me suis amusé à appliquer la méthode sur un tableur, avec une case pour indiquer la base...
Comme la "base d'Euler" est bancale (en tant que base...), il doit y avoir un petit souci de propagation des retenues, qui se compense, mais qui se voit sur la "goutte" qui tombe, la dernière : en base 10, pour les décimales 31 et 32, au lieu de 5 et 0, j'ai 4 et 10 ! (4*10+10 = 5*10+0).
Le programme C en tient compte : à chaque étape il écrit ce qu'il a calculé à l'itération précédente + l'éventuelle retenue de l'itération courante. Mais il ne prévoit pas qu'une retenue se propage sur deux niveaux...
Avec le tableur Calc, ça fonctionne en base 10 000 000, ce qui permet de calculer sept décimales à la fois. Au delà, il abandonne le calcul en nombres entiers pour passer au flottant...

J'ai modifié le programme C pour le faire bosser en base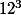
Désolé, mes modifs ne sont pas tout à fait aussi hermétiques que l'original
Ça donne ça :
#include
#include
unsigned long a=12*12*12,b,c=9000,d,e,f[9001],g,p;
char t[]="0123456789ab";
void main()
{
for(;b-c;)f[b++]=a/6;
for(;d=0,g=c*2;c-=12,p=e+d/a,printf("%c%c%c",t[p/144],t[(p/12)%12],t[p%12]),e=d%a)
for(b=c; d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);
}
Je pense avoir pris des précautions pour que les 2250 digits soient OK, mais bon...
(lire 3,1848... le programme ne met pas la virgule !)
3184809493b918664573a6211bb151551a057292
90a7809a492742140a60a55256a0661a03753a3a
a54805646880181a3683083272bbba0a370b1226
5529a828903b4b256b8403759a71626b8a546876
21849b849a8225616b442796a31737b229b23914
89853943b8763725616447236b027a421aa17a38
b52a18a838b01514a51144a23315a3009a8906b6
1b8b48a62253a88a50a43ba09445723159336644
76b3aabb77583975120683526b75b462060bb03b
432551913772729a2147553531793848a0402b99
9b5058535374465a68806716644039539a843193
5198527b9399b112990abb0383b107645424577a
51601b3624a88b7a676a3992912121a213887b92
873946a61332242217aa73541153577449391126
02ba4b888818a3269222b528487747839994ab22
3b65b8762695422822669ba00a586097842a5175
0362073b5a768363b21bb1a97a4a194447749399
804922175a068a46739461990a2065bb0a30bbab
7024a585b1a84428195489784a07a331a7b0a157
4565b373b05b03a5a80a13ab8785773467998555
8a5373178a7b28271992a3894a5776085083b9b2
38b2220542462888641a2bab8b3083ab49659172
a312b78518654494a068662586a181835a64440b
2970a12281397589881536720890580103288144
9223841428763329617531239b9a657405584014
534390b587625606bb80923795944b43757a431b
039556282978a6a49590553490ba184494717563
7a908247b50127722464441380a852b0847b5813
019bb70a67663b42656543406988447613219334
4ba55a2128a03838974606b851b2979321a40806
7225a5aa4b3464a1a17473595333909ab9127079
655b3164b68b9b28a9b818a220a025ab09342039
95b7a62a7aa739355340539ba3182905b1939056
03a43b660b9426a92294697144a896a5b2339358
bb2b7294bb89635b071a6351211360b820b1882a
b8433b54757b87a373284b1ba182a10326476b36
9a4a6365b58b8018994bb152556765475a704bb9
4b6b2a39458971a8b90512786b50294048186443
23552916170b3abb7363496427b088b68725a685
70040617949289077b278069a09b559324b8a668
28b40549b0296065b2300330592569a7b76b92ba
1293585b6a9b604567a0901362856373b4b56897
946256b4172b1b50474351364749a33996a81ba8
847347a8411b850b79a03018291672aa0945656a
159aa6aa0a845531a592005b8a34366b88225710
7b190969a846474836a9800750778920ba797297
a2791101b0685a86bb704b9baa17b05529367984
3b35215b0a8b1182b611953b080aa5431b219907
a8448a81b1a9493245676b88013b470335240859
594158621014216619553246570601967448b470
174b9244892444817453865a4003b5aa7176451a
ab90681a949786154aa040477382ba6937104171
0b8728458a23979252b254236753a44a1900aa28
3536a227648812525743868b410a567794663359
a6726a5286783328135114789b7645505b047848
020a730a9557b206776aa56a1968274410790130
6b29008808
BD :dingue2:
En fait, le programme C que tu exhibes applique l'algorithme en base 10000, ce qui lui permet d'afficher quatre chiffres à la fois.
Je me suis amusé à appliquer la méthode sur un tableur, avec une case pour indiquer la base...
Comme la "base d'Euler" est bancale (en tant que base...), il doit y avoir un petit souci de propagation des retenues, qui se compense, mais qui se voit sur la "goutte" qui tombe, la dernière : en base 10, pour les décimales 31 et 32, au lieu de 5 et 0, j'ai 4 et 10 ! (4*10+10 = 5*10+0).
Le programme C en tient compte : à chaque étape il écrit ce qu'il a calculé à l'itération précédente + l'éventuelle retenue de l'itération courante. Mais il ne prévoit pas qu'une retenue se propage sur deux niveaux...
Avec le tableur Calc, ça fonctionne en base 10 000 000, ce qui permet de calculer sept décimales à la fois. Au delà, il abandonne le calcul en nombres entiers pour passer au flottant...

J'ai modifié le programme C pour le faire bosser en base
Désolé, mes modifs ne sont pas tout à fait aussi hermétiques que l'original
Ça donne ça :
#include
#include
unsigned long a=12*12*12,b,c=9000,d,e,f[9001],g,p;
char t[]="0123456789ab";
void main()
{
for(;b-c;)f[b++]=a/6;
for(;d=0,g=c*2;c-=12,p=e+d/a,printf("%c%c%c",t[p/144],t[(p/12)%12],t[p%12]),e=d%a)
for(b=c; d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);
}
Je pense avoir pris des précautions pour que les 2250 digits soient OK, mais bon...
(lire 3,1848... le programme ne met pas la virgule !)
3184809493b918664573a6211bb151551a057292
90a7809a492742140a60a55256a0661a03753a3a
a54805646880181a3683083272bbba0a370b1226
5529a828903b4b256b8403759a71626b8a546876
21849b849a8225616b442796a31737b229b23914
89853943b8763725616447236b027a421aa17a38
b52a18a838b01514a51144a23315a3009a8906b6
1b8b48a62253a88a50a43ba09445723159336644
76b3aabb77583975120683526b75b462060bb03b
432551913772729a2147553531793848a0402b99
9b5058535374465a68806716644039539a843193
5198527b9399b112990abb0383b107645424577a
51601b3624a88b7a676a3992912121a213887b92
873946a61332242217aa73541153577449391126
02ba4b888818a3269222b528487747839994ab22
3b65b8762695422822669ba00a586097842a5175
0362073b5a768363b21bb1a97a4a194447749399
804922175a068a46739461990a2065bb0a30bbab
7024a585b1a84428195489784a07a331a7b0a157
4565b373b05b03a5a80a13ab8785773467998555
8a5373178a7b28271992a3894a5776085083b9b2
38b2220542462888641a2bab8b3083ab49659172
a312b78518654494a068662586a181835a64440b
2970a12281397589881536720890580103288144
9223841428763329617531239b9a657405584014
534390b587625606bb80923795944b43757a431b
039556282978a6a49590553490ba184494717563
7a908247b50127722464441380a852b0847b5813
019bb70a67663b42656543406988447613219334
4ba55a2128a03838974606b851b2979321a40806
7225a5aa4b3464a1a17473595333909ab9127079
655b3164b68b9b28a9b818a220a025ab09342039
95b7a62a7aa739355340539ba3182905b1939056
03a43b660b9426a92294697144a896a5b2339358
bb2b7294bb89635b071a6351211360b820b1882a
b8433b54757b87a373284b1ba182a10326476b36
9a4a6365b58b8018994bb152556765475a704bb9
4b6b2a39458971a8b90512786b50294048186443
23552916170b3abb7363496427b088b68725a685
70040617949289077b278069a09b559324b8a668
28b40549b0296065b2300330592569a7b76b92ba
1293585b6a9b604567a0901362856373b4b56897
946256b4172b1b50474351364749a33996a81ba8
847347a8411b850b79a03018291672aa0945656a
159aa6aa0a845531a592005b8a34366b88225710
7b190969a846474836a9800750778920ba797297
a2791101b0685a86bb704b9baa17b05529367984
3b35215b0a8b1182b611953b080aa5431b219907
a8448a81b1a9493245676b88013b470335240859
594158621014216619553246570601967448b470
174b9244892444817453865a4003b5aa7176451a
ab90681a949786154aa040477382ba6937104171
0b8728458a23979252b254236753a44a1900aa28
3536a227648812525743868b410a567794663359
a6726a5286783328135114789b7645505b047848
020a730a9557b206776aa56a1968274410790130
6b29008808
BD :dingue2:
LeJeu a écrit:Pour les fous furieux.. : qui me donnerait le plus grand nombre de décimales de Pi en base 12 ?
Kolossal !
Un gars qui bosse en base 12^3 ne peut pas être foncièrement mauvais !
Tu viens certainement de gagner ta place au paradis des fous furieux
Très beau travail - je vais relire ça tranquillement .
[CENTER]BEN318 : tu as déjà eu un plus beau cadeau pour ta fête ?[/CENTER]
LeJeu a écrit:Un gars qui bosse en base 12^3 ne peut pas être foncièrement mauvais !
Tu viens certainement de gagner ta place au paradis des fous furieux
J'en suis sincèrement fort aise !
LeJeu a écrit:je vais relire ça tranquillement .
En fait, j'avais chaussé mes gros sabots pour faire ça, mais je réfléchis à une frappe plus chirurgicale.
1/ Profondeur de calcul : le poids des digits est divisé par
2/ c-=12...
Le programme abandonne une partie des digits de poids faible au fur et à mesure de sa progression. C'est grosso modo le nombre de digits Euler qui ont de l'influence sur un digit en sortie. Je suis passé de 14 à 12 au jugé : ça doit pouvoir être grandement optimisé. le log2() de la base doit être le bon ordre de grandeur.
En fait, le nombre de digits en "base Euler" est le produit de c par le nombre de chiffres en sortie.
3/ 2250 digits
Ca correspond à peu près sauf erreur de ma part aux 2400 digits décimaux (2400*log(10)/log(12))
4/ une clé : f[b++]=a/6
C'est une horreur héritée du programme original pour initialiser le tableau, qui ne fonctionne qu'en base paire. La bonne expression serait ici 2 * 12 ^(3-1).
Ça permet de sortir autant de digits le premier coup que les autres fois (ici 3 : 318).
5/ Je n'ai pas encore d'idée précise de la valeur max des nombres en uvre dans l'algorithme en fonction de la base (pour les débordements des calculs en entier). Mais ça viendra peut-être.
Bonne journée.
BD
Avant de passer à autre chose, et après avoir modifié le programme pour le rendre plus général et lui permettre de tourner en 64 bit :
Les 499 premières et 501 dernières parmi 1 000 000 duodécimales (base 12) calculées en base 743008370688 en 1h17 :
[FONT=Courier New]
3.
184809493b918664573a6211bb151551a05729290a7809a49
2742140a60a55256a0661a03753a3aa54805646880181a3683
083272bbba0a370b12265529a828903b4b256b8403759a7162
6b8a54687621849b849a8225616b442796a31737b229b23914
89853943b8763725616447236b027a421aa17a38b52a18a838
b01514a51144a23315a3009a8906b61b8b48a62253a88a50a4
3ba0944572315933664476b3aabb77583975120683526b75b4
62060bb03b432551913772729a2147553531793848a0402b99
9b5058535374465a68806716644039539a8431935198527b93
99b112990abb0383b107645424577a51601b3624a88b7a676a
...
47a96a2a469123659933074a344965389787802b356a320242
77b9b2512aa263888150a86879279365708a940b465503b147
1011748b136751ab73128a941a70a3953b2923a22511317903
92bb7a547484387244b7686b10338a770b88b9820bb7271b60
0b3503a8a41b7b06865a96b825a9815280b1671658859654b3
583a9793345903516a89564607158b89a00a09b09b49b72269
b6a4731647242b744847806621b697169960b00907029b3679
64156606b3799580b93868ab92a261929b935b8a6227856a99
9bb24a075660a45ab182855a40794b4a645a71939103408714
882365388823aa4903b76b311843975b152bb09410bb8a6831
4
[/FONT]
et les 999 premières (base 37) parmi 100 000 calculées en base 3512479453921, le jeu de chiffres étant :
(base 37) parmi 100 000 calculées en base 3512479453921, le jeu de chiffres étant :
0123456789abcdefghijklmnopqrstuvwxyz_
J'espérais y trouver mon épitaphe au cas où pi serait un nombre univers, mais rien de tel pour le moment...
[FONT=Courier New]
3.
58v3fwnjb6u483qxykn7vp8hoss1mo4wr_p71y5hh_x2shug_
vrs7_sg4a8ttl_dfuvemsfwbnqx2c9p4s2rlpgyfjc7ftpzn66
v3z0kagbcvmabu50afyx1x_wdlrwq13hmxmh7ioxjb9lv8gtw4
gl3rtb_p0jo2kq7ze6rkbu345054p4_xhdun2nd43mjle0jzn7
yu4gzf4pmx2tx8lznmdtmjwjejegskq6x28qel00datyj_hv1p
ys38sluuiswy2jzzs8v3w_fyixhfvut240fbrhq87uo4oyx5w9
rm6_y1ppr4oz5t7ihe1b5t1hyp5sg2u8br0kdtmdu_gsr8lv03
73k5ijhulbzwrsyg51j2pkd1j8odx3lh4xkxzb7br4nmlmid0d
p3mnyz5nqfqefa02dn11edz7nmq3cjig9b2gtiuzkhwcm201lo
g2ga9uex65_w99sm8aw0r3lleh0pajif68zj8bx2mq852irfnk
slavyu8b0eslezz_4wfe4fzi_o32v7md8uktdel3iqitscbwdj
2dykez076juwl4w8u720rt9vqoez4p1mgawt3wlrqqr2awl5au
h71zv23dga4qq5yfxjq6dla9wnvmk28p5nkf64m6cuo13svm5s
2rhybvsrxr0i_1dgzrwv3nktin3xt328no54sxnqip3sfu7zus
ssinb9brrzpm5qhx9_r6x8glqe9rihdf6tx_r3syr7wvw1i2m4
bhov7sz1j24sbb7rz5qj0ah6hvu597cljorkazazp5f2g123a6
2d629mi9h8u5o5zetzqhw245897bd1v4ecejrhsnfi8dzu7im_
xqphgz_78pqobwci25ri6f8sl9fn69anteejvdrt_bnwwhq8bd
xxkaszlbe8p29dnpz8oq_b6z90rhsi89eqwvqv4s46jlv1n3gb
980di9gkdunnn_xwhb7m98olpb7tnpyguuxnol6z822mp0yt2g
[/FONT]
Le temps d'exécution de l'algorithme est proportionnel au carré du nombre de digits.
BD :arf: :dingue: :party:
Les 499 premières et 501 dernières parmi 1 000 000 duodécimales (base 12) calculées en base 743008370688 en 1h17 :
[FONT=Courier New]
3.
184809493b918664573a6211bb151551a05729290a7809a49
2742140a60a55256a0661a03753a3aa54805646880181a3683
083272bbba0a370b12265529a828903b4b256b8403759a7162
6b8a54687621849b849a8225616b442796a31737b229b23914
89853943b8763725616447236b027a421aa17a38b52a18a838
b01514a51144a23315a3009a8906b61b8b48a62253a88a50a4
3ba0944572315933664476b3aabb77583975120683526b75b4
62060bb03b432551913772729a2147553531793848a0402b99
9b5058535374465a68806716644039539a8431935198527b93
99b112990abb0383b107645424577a51601b3624a88b7a676a
...
47a96a2a469123659933074a344965389787802b356a320242
77b9b2512aa263888150a86879279365708a940b465503b147
1011748b136751ab73128a941a70a3953b2923a22511317903
92bb7a547484387244b7686b10338a770b88b9820bb7271b60
0b3503a8a41b7b06865a96b825a9815280b1671658859654b3
583a9793345903516a89564607158b89a00a09b09b49b72269
b6a4731647242b744847806621b697169960b00907029b3679
64156606b3799580b93868ab92a261929b935b8a6227856a99
9bb24a075660a45ab182855a40794b4a645a71939103408714
882365388823aa4903b76b311843975b152bb09410bb8a6831
4
[/FONT]
et les 999 premières
0123456789abcdefghijklmnopqrstuvwxyz_
J'espérais y trouver mon épitaphe au cas où pi serait un nombre univers, mais rien de tel pour le moment...
[FONT=Courier New]
3.
58v3fwnjb6u483qxykn7vp8hoss1mo4wr_p71y5hh_x2shug_
vrs7_sg4a8ttl_dfuvemsfwbnqx2c9p4s2rlpgyfjc7ftpzn66
v3z0kagbcvmabu50afyx1x_wdlrwq13hmxmh7ioxjb9lv8gtw4
gl3rtb_p0jo2kq7ze6rkbu345054p4_xhdun2nd43mjle0jzn7
yu4gzf4pmx2tx8lznmdtmjwjejegskq6x28qel00datyj_hv1p
ys38sluuiswy2jzzs8v3w_fyixhfvut240fbrhq87uo4oyx5w9
rm6_y1ppr4oz5t7ihe1b5t1hyp5sg2u8br0kdtmdu_gsr8lv03
73k5ijhulbzwrsyg51j2pkd1j8odx3lh4xkxzb7br4nmlmid0d
p3mnyz5nqfqefa02dn11edz7nmq3cjig9b2gtiuzkhwcm201lo
g2ga9uex65_w99sm8aw0r3lleh0pajif68zj8bx2mq852irfnk
slavyu8b0eslezz_4wfe4fzi_o32v7md8uktdel3iqitscbwdj
2dykez076juwl4w8u720rt9vqoez4p1mgawt3wlrqqr2awl5au
h71zv23dga4qq5yfxjq6dla9wnvmk28p5nkf64m6cuo13svm5s
2rhybvsrxr0i_1dgzrwv3nktin3xt328no54sxnqip3sfu7zus
ssinb9brrzpm5qhx9_r6x8glqe9rihdf6tx_r3syr7wvw1i2m4
bhov7sz1j24sbb7rz5qj0ah6hvu597cljorkazazp5f2g123a6
2d629mi9h8u5o5zetzqhw245897bd1v4ecejrhsnfi8dzu7im_
xqphgz_78pqobwci25ri6f8sl9fn69anteejvdrt_bnwwhq8bd
xxkaszlbe8p29dnpz8oq_b6z90rhsi89eqwvqv4s46jlv1n3gb
980di9gkdunnn_xwhb7m98olpb7tnpyguuxnol6z822mp0yt2g
[/FONT]
Le temps d'exécution de l'algorithme est proportionnel au carré du nombre de digits.
BD :arf: :dingue: :party:
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
