Billet vert
Olympiades mathématiques, énigmes et défis
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 08 Mar 2013, 13:32
par LeJeu » 08 Mar 2013, 13:32
Imod a écrit:Nhésites pas à donner la suite quand tu trouveras un peu de temps .
Imod
Je confirme que si on ne perd pas dans lescalculs on arrive sur le résultat, trois jours en retard sur galax.....détails ce soir
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 08 Mar 2013, 13:39
par LeJeu » 08 Mar 2013, 13:39
Doraki a écrit:vous parlez de volumes mais le dessin est en 2D.
Le problème est-il en 2D ou en 3D ?
Le pb initial est en 3d. Mais tu as raison si on travaille sur la coupe en 2d ça doit marcher aussi bien.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 08 Mar 2013, 18:14
par chan79 » 08 Mar 2013, 18:14
Salut
Finalement, j'arrive à ça:
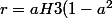-\sqr{9(1-a^2)^2-3(6a^3-9a^2+3)}\)}{6a^3-9a^2+3})
H hauteur du cône
a est le sinus de
 Heureusement, ça se simplifie
Heureusement, ça se simplifie :
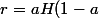(2a+1)})

-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 08 Mar 2013, 19:41
par Imod » 08 Mar 2013, 19:41
Bonsoir à tous :zen:
Je viens de me rendre compte que j'ai été involontairement très injuste pour ce site . J'ai proposé le même problème sur deux autres sites en fournissant les liens .
Je répare mon erreur avec toutes mes excuses
 îles des mathsLes maths.net
îles des mathsLes maths.netImod
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 08 Mar 2013, 19:55
par LeJeu » 08 Mar 2013, 19:55
LeJeu a écrit:Le pb initial est en 3d. Mais tu as raison si on travaille sur la coupe en 2d ça doit marcher aussi bien.
Je dis bien sûr n'importe quoi, on ne peut bien sur pas travaillet qu'en 2D , ce n'est pas parce que la surface de coupe est maximum que le volume le sera !!!!
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 08 Mar 2013, 20:04
par Doraki » 08 Mar 2013, 20:04
on fixe l'olive et le sommet en bas du verre (donc on fixe la hauteur Y du centre de l'olive et son rayon R).
On appelle H la différence entre le haut du verre et le centre de l'olive, et on fait varier H.
On appelle 2B la longueur du segment rouge du bas sur le dessin d'Imod, A la longueur du segment rouge sur les cotés, R1 le rayon en haut du verre, et R2 le rayon du cercle de l'intersection de l'olive avec le haut du verre.
R2 vérifie R2² + H² = R², (ce qui permet de calculer R2 en fonction de H et R)
En regardant le dessin on voit 4 triangles rectangles semblables : les 4 triplets
[R² ; Y²-R² ; Y² ]
[R1² ; (H+Y)² ; R1²+(H+Y)²]
[B² ; (Y-R)² ; B²+(Y-R)²]
[(R1-B)² ; (H+R)² ; A²]
sont proportionnels entre eux, ce qui permet de calculer B en fonction de R et Y, A et R1 en fonction de H,R,Y.
En particulier, la condition d'égalité des deux longueurs rouges devient
A² = 4B²
<=> A²(Y²-R²) = 4B²(Y²-R²)
<=> (H+R)²Y² = 4(Y-R)²R²
<=> (H+R)Y = 2R(Y-R)
<=> HY = R(Y-2R).
On appelle V1 le volume du verre et V2 le volume de la portion d'olive comprise dans le verre.
on cherche le maximum de V2/V1. Celui-ci s'obtient lorsque dV1*V2 = dV2*V1, soit dV1/dV2 = V1/V2.
dV1 = ;)R1²dH, dV2 = ;)R2²dH, V1 = ;)(H+Y)R1²/3, donc tout ça équivaut à V2 = ;)(H+Y)R2²/3 :
Si on préfère des beaux raisonnements on dit que le maximum s'atteint lorsque V2 est au disque de rayon R2 ce que V1 est au disque de rayon R1: V2 = le volume du cône de hauteur (H+Y) et de base le disque de rayon R2.
Un calcul d'intégrale (j'crois pas qu'on puisse y échapper) donne
V2 = ;) intégrale de -R à H de (R²-x²) dx
= ;)(H+R)[R² - (H²-HR+R²)/3]
= ;)(H+R)(2R²+2RH-RH-H²)/3
= ;)(H+R)²(2R-H)/3
(moi en tout cas je savais pas que le volume d'une sphère tronquée était le volume du cône de hauteur 2R-H et de base un disque de rayon H+R)
On obtient donc la condition (H+R)²(2R-H) = (H+Y)R2² = (H+Y)(R²-H²),
<=> (H+R)(2R-H) = (H+Y)(R-H)
<=> 2R² = RY-HY (on note la simplification miraculeuse de H²)
<=> HY = R(Y-2R).
On obtient bien la même chose, et je sais vraiment pas comment t'as intuité cette équivalence avec l'égalité des longueurs rouges.
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 08 Mar 2013, 20:15
par LeJeu » 08 Mar 2013, 20:15
LeJeu a écrit:Je confirme que si on ne perd pas dans lescalculs on arrive sur le résultat, trois jours en retard sur galax.....détails ce soir
soit x hauteur immergé
la surface de la sphère immergée est x* 2 PI R
surface du disque à la surface est pi ( 2 xR -x²)
les volumes égaux donnent:
2R dr = (2R-x) dh
avec dr = dh*sin(a)
donc (1) : 2R ( sin(a) -1) = - x
avec la relation trigo dans le verre
sin a = R /(h -x+R)
donc (2) : -x = R/sin(a) -R -h
on égale(1) et ( 2)
2R ( sin(a) -1) = R( 1/sin(a) -1) -h
ce qui donne R :
}{(1-sin( a) )(2sin(a) +1)})
Ce qui semble la formule attendue, par contre je ne comprends pas pourquoi je trouve du 2 sin(a)+1 au dénominateur ? j'attendais du 2 sin(a)-1 pour trouver une forme indéterminée pour a =pi /6
une idée ?
[edit] correction du signe de h temporairement faux....
et x aussi
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 08 Mar 2013, 20:28
par LeJeu » 08 Mar 2013, 20:28
Doraki a écrit:On obtient bien la même chose, et je sais vraiment pas comment t'as intuité cette équivalence avec l'égalité des longueurs rouges.
Moi non plus ...
Il me semble qu'en adaptant mon calcul précédent ( qui fait semblant de ni intégrer, ni dériver

)
On doit pouvoir montrer que le plan horizontal passant par le cercle de contact de la sphère est à équidistance du plan de la surface et du plan passant par le point le plus bas de la sphère ?
ce qui si j'ai bien compris est la proposition de Imod ?
Mais franchement pas sûr sur ce coup là ( d'y arriver !)
-
LeJeu
- Membre Irrationnel
- Messages: 1142
- Enregistré le: 24 Jan 2010, 21:52
-
 par LeJeu » 08 Mar 2013, 21:07
par LeJeu » 08 Mar 2013, 21:07
LeJeu a écrit:On doit pouvoir montrer que le plan horizontal passant par le cercle de contact de la sphère est à équidistance du plan de la surface et du plan passant par le point le plus bas de la sphère ?
Je crois que j'ai...
on part de 2R ( sin(a) -1) = - x
qui est la condition pour que le volume soit optimum en fonction de x ( voir post précédent)
on pose x =u +v
u : hauteur immergée au dessus du point de contact
v : hauteur immergée en dessous du point de contact
un coup de trigo nous donne v =R( 1-sin(a))
=> 2R ( sin (a) -1) = - ( u + R(1-sin(a))
u = R(1 - sin (a))
ce que l'on cherchait!
Il me semble que c'est plutot sympa comme calcul.
Imod, est ce que c'est ce que tu appelles :
"une justification ' physique ' ou au moins qualitative" ?
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 08 Mar 2013, 22:47
par Imod » 08 Mar 2013, 22:47
Doraki a écrit:On obtient bien la même chose, et je sais vraiment pas comment t'as intuité cette équivalence avec l'égalité des longueurs rouges.
Si je le savais ...
Mais bon , il y a un petit moment , j'ai passé plusiuers semaines sur un problème d'isopérimétrie mettant en jeu ce trapèze . Naturellement je l'ai cherché ici et s'il colle au problème ce n'est peut-être pas un hasard .
Merci de tintéresser au problème :we:
Imod
-
Imod
- Habitué(e)
- Messages: 6484
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 08 Mar 2013, 23:04
par Imod » 08 Mar 2013, 23:04
LeJeu a écrit:Imod Qu'est-ce que tu appelles : "une justification ' physique ' ou au moins qualitative" ?
Les solutions des problèmes de minimum ou maximum présentent souvent des symétries qu'on peut justifier plus ou moins "physiquement" . C'est apparemment le cas ici :zen:
Imod
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 09 Mar 2013, 00:03
par Doraki » 09 Mar 2013, 00:03
Ou pourrait dessiner le verre "symétrique" où on échange les deux longueurs rouges voir si il y a des trucs à dire (et où on garde le même angle du verre, et le même rayon pour la sphère).
Le mieux serait de montrer que le rapport volume de la sphère / volume du verre est inchangé mais çe ne m'a pas l'air de donner des calculs très simples. Déjà je sais même pas si c'est vrai.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 28 Déc 2013, 17:39
par Ben314 » 28 Déc 2013, 17:39

Bon, j'ai encore foiré la taillle du dessin...
J'ai une preuve un peu plus directe, mais les simplifications "magiques" restent quand même un peu mystèrieuses...
Sur le dessin on "lit" que :
1)
\)
donc
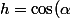a)
2)
\)
donc
 <br />= \frac{b}{2} \times \frac{1+\cos( \frac{\pi}{2} - \alpha )} {\sin(\frac{\pi}{2}-\alpha)} <br />= \frac{1+\sin(\alpha )} {2\cos(\alpha)} b)
3)
a=AB)
Le volume de la portion de sphère intérieure au verre est :
^2\big)dt<br />=\frac{\pi}{3}h^2(3r-h)<br />=\frac{\pi}{3}\big(\cos(\alpha)a\big)^2\big(3 \frac{1+\sin(\alpha )} {2\cos(\alpha)}b-\cos(\alpha)a\big))
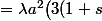b-2c^2 a\big)\)
où
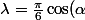)
est une constante,
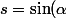)
et
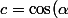)
.
On en déduit que :
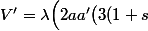b-2c^2 a\big)+a^2\big(3(1+s)b'-2c^2 a'\big) \Big))
Or la relation 3) implique que
a'=0\)
c'est à dire
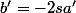
donc
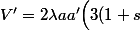b-2c^2 a+a\big(-3s(1+s)-c^2\big) \Big)<br />=6(1+s)\lambda a a'(b-a))
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
