Axiomes réduits de la structure de groupe

[tournesol]

Bonjour à tous
Soit E non vide muni d'une LDCI que l'on notera multiplicativement
Montrer que (E,loi) est un groupe ssi
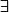
x,y,z E (xy)z=x(yz) et tE xty=z

[catamat]

Bonjour
Intéressant!

Je me lance pour l'élément neutre...

Soit y élément de E, il existe T élément de E tel que yTy=y
donc yTyT = yT
Notons e cet élément yT qui vérifie ee=e

Soit x un élément de E, il existe t élément de E tel que xte=x
donc xtee=xe
ou xte=xe puisque ee=e
or xte=x
donc x=xe

De même il existe u élément de E tel que eux=x
donc eeux=ex
ou eux = ex
et donc x=ex

On a pour tout élément x de E, ex=xe=x, e est élément neutre pour cette loi

[tournesol]

Bien vu catamat
Que peux tu alors dire de y ?

[GaBuZoMeu]

Bonjour,

Quel y ?

Une fois qu'on a un élément neutre e, c'est quasiment fini : chaque élément x a un inverse à droite t (tel que xte=e) et un inverse à gauche u (tel que eux=e) et u=u(xt)=(ux)t=t.

[tournesol]

Bonsoir ,
catamat écrit yT=e donc y est inversible à droite.
Mais TyTy=Tey=Ty
Donc Ty=e' vérifie e'e'=e' et on a déjà montré qu'une telle propriété impliquait la neutralité de e' et comme un neutre c'est unique , CQFD

[catamat]

Merci Tournesol, je ne connaissais pas du tout ou alors j'ai oublié