Assez difficile mais sympa

[MMu]

Soient un réel et une suite réelle telle que .
Montrer qu'il existe un et un seul telle que la suite soit convergente vers une limite finie strictement positive . ...

[Ben314]

Salut,
Je pense avoir une soluce :
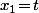
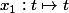
On regarde (évidement) les comme étant des fonctions de la variable , c'est a dire en fait qu'on considère la fonction et qu'on regarde la formule de récurrence comme définissant la fonction en partant de la fonction .

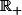
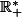
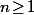
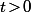
Il est clair (récurrence) que les fonctions sont des homéomorphismes strictement croissant de sur lui même et qu'elle sont sur . Pour tout et tout (donc ) on a alors les équivalences suivantes :
qui est en fait l'abscisse de l'unique point d'intersection (autre que (0,0)) des courbes de et de .
On a alors donc .
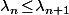
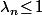
Mais d'un autre coté, il est clair (récurrence) que pour tout donc ce qui garantie que la suite converge vers un certain .

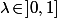
On va montrer que la suite
(1) tend vers 0 si
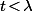
(2) tend vers si
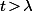
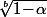
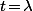
(3) tend vers si (où est la limite de la suite décroissante et minorée )


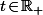
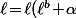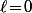
Constatons déjà que, si pour un certain la suite converge vers un réel alors, en passant à la limite dans la formule de récurrence, on obtient donc ou bien .

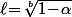
(1) Considérons un .
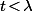
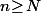
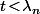
Par définition d'une limite, il existe un tel que, pour tout , on ait ce qui implique que la suite est décroissante à partir du rang N donc convergente (car minorée par 0) vers une limite .
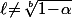
Mais donc et on a forcément

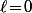
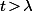
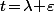
(2) Considérons un et écrivons avec .
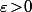
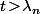
On a évidement pour tout (car est croissante) ce qui signifie que est croissante.
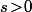
D'un autre coté, on a évidement pour tout et la formule de récurrence permet de voir que (l'autre terme dans la dérivée du produit est positif).
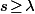
Pour tout on a alors et on en déduit (par récurrence) que pour tout .
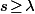
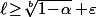
Le T.A.F. nous dit alors que ce qui signifie que si la suite (croissante) convergeait vers un réel on devrait avoir ce qui est impossible.
Donc la suite tend vers .

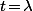
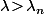
(3) Si alors pour tout donc est croissante.
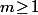
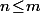
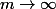
D'un autre coté, si on fixe un , la suite est croissante de 1 à (puis décroissante) ce qui signifie que pour tout on a et en prenant la limite de cette inégalité lorsque (avec fixé) on en déduit que . Cela assure que la suite est convergente et, comme sa limite ne peut être 0 (elle est croissante), c'est forcément

[FLBP]

Bonsoir,

Si on prend la réciproque de la méthode du point fixe :





La suite converge si :











Cordialement.

[Ben314]

Si on prend la réciproque de la méthode du point fixe :

Tu n'auras pas légèrement oublié le "détail" consistant à voir que la fonction définissant en fonction de dépend elle même de (à cause du ) ?
Si ce n'était pas le cas, alors dans ma prose çi dessus la suite serait constante et effectivement, il n'y aurait quasiment rien à dire...

[MMu]

OK Ben ,c'est bon.. (par contre je ne comprends pas le message de FLBP).
Comme Ben, on montre l'existence avec . Pour le fun , voici une autre méthode pour l'unicité.
On observe que et est une fonction convexe donc .
Supposons solutions du problème donc
De par la convexité on a . En passant à la limite on obtient donc et finalement ..

[FLBP]

Merci, Ben, oui je me suis trompé, ça ne marche que pour constant ... Et bravo pour ta démonstration