[demande d'exos]Arithmétique
26 messages
- Page 1 sur 2 - 1, 2
[demande d'exos]Arithmétique
Bonjour,
est ce que vous avez des exos d'arithmétique bien difficiles et dont la solution peut etre élémentaire et élégante ?
Lapras
est ce que vous avez des exos d'arithmétique bien difficiles et dont la solution peut etre élémentaire et élégante ?
Lapras
Ouais ça devrait l'occuper au moins cet après-midi :langue2:
Sinon tu prends un exo et tu essayes de le généraliser. Par exemple trouver d'autres valeurs de a telles que la suite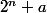 ait une infinité de termes premiers deux à deux (perso, j'en vois déjà deux
ait une infinité de termes premiers deux à deux (perso, j'en vois déjà deux  ) ou trouver un a (non pair ....) tel que ce ne soit jamais le cas.
) ou trouver un a (non pair ....) tel que ce ne soit jamais le cas.
Sinon tu prends un exo et tu essayes de le généraliser. Par exemple trouver d'autres valeurs de a telles que la suite
Bien ! Un peu bourrin avec la théorie algébrique des nombres, mais bon !
Autre manière de faire : On suppose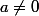 et
et 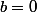 . Par hypothèse, il existe des entiers
. Par hypothèse, il existe des entiers  et
et  tels que :
tels que : 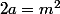 et
et 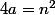 , d'où
, d'où 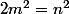 ou encore
ou encore 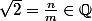 : Absurde. Donc
: Absurde. Donc 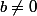 .
.
On considère maintenant les suites et
et  définies de la manière suivante :
définies de la manière suivante : =\left(2\sqrt{2^{n}a+b}, \sqrt{2^{n+2}a+b}\right)) . Clairement :
. Clairement : (x_n-y_n) = 3b) , donc pour tout
, donc pour tout  ,
, 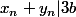 . Or pour
. Or pour  assez grand,
assez grand, 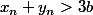 , contradiction, donc nécessairement,
, contradiction, donc nécessairement, 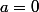 .
.
Autre manière de faire : On suppose
On considère maintenant les suites
Hmm, pour tout p premier différent de 2,
la suite (2^n) est dense dans l'ensemble des inversibles de Zp (les nombres p-adiques)
Donc comme f est continue, l'image par f d'un inversible est dans l'adhérence de l'ensemble des carrés, donc inclus dans l'ensembles des nombres de valuation p-adique paire.
Du coup, la valuation p-adique de n'importe quel f(x) est paire sauf peut-être pour p=2 ou p divisant f(0)
(Si p est différent de 2 et si p est un facteur premier de f(x) et si x n'est pas inversible, ça veut dire que x = 0 mod p, et donc que f(0) = 0 mod p, donc p divise f(0))
Si f(0) = 0 alors en regardant la 2-valuation du coefficient de X, on voit qu'elle doit être infinie, et donc que le coefficient est nul. Donc on peut diviser f par X².
Maintenant si f(0) n'est pas nul : soit k la 2-valuation de f(0) (paire car 0 c'est la limite des 2^n)
Soit donc (un) = (an+b) une sous-suite arithmétique de (n*2^(k+1)) qui ne contient aucun multiple de p pour p premier > 2 divisant f(0).
Pour tout n, f(un) est un carré car toutes ses p-valuations sont paires.
Donc f composé avec (x -> ax+b) est un polynome dont toutes les valeurs sont des carrés, c'est donc le carré d'un polynome.
Donc f est le carré d'un polynome à coefficients rationnels, mais comme il est à coefficients entier, f est le carré d'un polynôme à coefficients entiers.
la suite (2^n) est dense dans l'ensemble des inversibles de Zp (les nombres p-adiques)
Donc comme f est continue, l'image par f d'un inversible est dans l'adhérence de l'ensemble des carrés, donc inclus dans l'ensembles des nombres de valuation p-adique paire.
Du coup, la valuation p-adique de n'importe quel f(x) est paire sauf peut-être pour p=2 ou p divisant f(0)
(Si p est différent de 2 et si p est un facteur premier de f(x) et si x n'est pas inversible, ça veut dire que x = 0 mod p, et donc que f(0) = 0 mod p, donc p divise f(0))
Si f(0) = 0 alors en regardant la 2-valuation du coefficient de X, on voit qu'elle doit être infinie, et donc que le coefficient est nul. Donc on peut diviser f par X².
Maintenant si f(0) n'est pas nul : soit k la 2-valuation de f(0) (paire car 0 c'est la limite des 2^n)
Soit donc (un) = (an+b) une sous-suite arithmétique de (n*2^(k+1)) qui ne contient aucun multiple de p pour p premier > 2 divisant f(0).
Pour tout n, f(un) est un carré car toutes ses p-valuations sont paires.
Donc f composé avec (x -> ax+b) est un polynome dont toutes les valeurs sont des carrés, c'est donc le carré d'un polynome.
Donc f est le carré d'un polynome à coefficients rationnels, mais comme il est à coefficients entier, f est le carré d'un polynôme à coefficients entiers.
salut, il y a un site avec les exos d'OIM depuis 1959 si tu veux : http://imo.math.ca/oim.html
et sinon j'avais trouvé un PDF avec pleins d'exo d'olympiades nationales (environ 150 pages lol tu aurais trouvé ton bonheur) mais je ne le trouve plus, je vais encore cherché
et sinon j'avais trouvé un PDF avec pleins d'exo d'olympiades nationales (environ 150 pages lol tu aurais trouvé ton bonheur) mais je ne le trouve plus, je vais encore cherché
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
