Arithmétique

[Doraki]

Bon je le remets puisque ça a été supprimé :

Montrer que l'équation (x²+23)(x^3-x-1) = 0 a une solution modulo n pour tout n>=1, mais pas de solution dans Q.

[ffpower]

Je suppose que le fait que 27*(-1)²+4(-1)^3=23 n'est pas étranger à l'affaire..

[Doraki]

A tes erreurs de signe près dans tes discriminants, c'est en effet plus qu'une coïncidence.

[ffpower]

Bon, histoire de faire avancer le shmilblick: j'ai la conclusion si n est premier et que -3 n'est pas un carré modulo n (bah quoi c'est toujours ça de fait^^)

Bref, j'utilise les formules de Cardan pour résoudre X^3-X-1=0, j'obtiens:

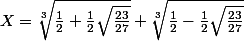
(affiche un truc bizarre en second membre..si quelqu'un voit le bug dans mon code latex qu'il le dise, moi j'arrive pas à le voir..)

Après je dis que dans mon contexte, X^3=1 n'a que 1 comme solution et j'en déduis que x->x^3 est injectif donc bijectif, ce qui permet de définir la racine cubique dans Z/nZ. Si on suppose de plus que X^2+23 n'a pas de racines, donc que -23 n'est pas un carré, alors ni -3 ni -23 sont des carrés donc
23/27=(-23)*(-3)/9² est un carré..Ainsi tous les termes dans Cardan peuvent être définis dans Z/nZ et on a donc une racine de X^3-X-1 modulo n.

[Benjamin]

Salut,

Il n'y a pas d'erreur. Voici la formule grâce au site suivant.
[img]http://latex.codecogs.com/gif.latex?X=\sqrt[3]{\frac{1}{2}+\frac{1}{2}\sqrt{\frac{23}{27}}}+\sqr%20%20t[3]{\frac{1}{2}-\frac{1}{2}\sqrt{\frac{23}{27}}}[/img]

[Olympus]

Salut !

@Benjamin : euh ça c'est parce que tu l'as recopiée avec l'espace entre "\sqr" et "t", qui ne figure pas dans le message de ffpower et que mimeTeX semble avoir ajouté tout seul. Sinon, je viens de modifier son message et corrigé la formule, sans comprendre la logique, il semble que mimeTeX traduit "+\sqrt[3]" en "+\sqr t[3]", et "+ \sqrt[3]" ( espace entre + et \ ) en la racine cubique du machin.

[ffpower]

Thanks Olympus :we:

Et gloire à MimeTeX :ptdr:

[Doraki]

Je crois que mimeTex met un espace tout seul quand il voit une suite de 60 caractères collés sans espaces.

A part ça, ouais t'as fait les 3/4 faciles, il reste le quart non trivial où -23 n'est pas un carré, et -3 est un carré.
Là il va falloir faire un minimum de théorie de Galois.

[ffpower]

Hum..c'est ce que je craignais^^
Bon, j'essaierai mais..moi et la théo de Galois :hum:

[ffpower]

Bon aprés avoir googliser un peu de théo de Galois sur corps finis..^^

Il semblerait donc que sur les corps finis, les groupes de Galois sont toujours cycliques. A partir de là, si je dis pas de bétise, si on suppose que X^3-X-1 est irréductible, son corps de décomposition K ne peut pas être de degré 6, car le groupe de Galois du polynome serait S_3 sinon, donc non cyclique.

Du coup le corps de décomposition K est de degré 3 sur F_p. Après si on note x,y,z les 3 racines du poly et A=(x-y)(x-z)(y-z), on a A²=-23. Donc A est un élément de K de degré au plus 2 sur F_p, mais puisque [K:F_p]=3, A est en fait dans F_p, et X²+23 a donc une racine.

[ffpower]

Tripost^^

En fait on peut se passer de Galois: Soit K le corps de décomposition de X^3-X-1 (supposé irréductible) et L={x dans K tq x^{p^3}=x} l'unique sous corps de degré 3 sur Fp. Les racines du polynomes étant de degré 3 sur F_p, elles appartiennent toutes à L et donc K=L et donc [K:Fp]=3

[Doraki]

oui voilà.

Si X^3-X-1 est irréductible mod p, alors Fp^3 = Fp[x]/(x^3-x-1) contient toutes les racines de X^3-X-1 (à savoir x, x^p et x^p²) et donc il contient a = sqrt(-23).
Donc -23 est un carré dans Fp^3, donc c'était un carré dans Fp.

[ffpower]

Plus simple que Cardan au final^^

Le cas n quelconque se déduit du cas n premier?

[Doraki]

Ben avec le cas p premier, tu fais le cas p^n (en faisant gaffe pour p=2 et p=23), et ensuite le cas n quelconque.