Arithmétique : coefficients binomiaux

[lapras]

Soit n un entier positif ou nul tel que pour tout 0 <= k <= n, (k , n) est impair.
Montrer que n = 2^m 1 pour un entier m.

(k , n) c'est "k parmis n" (ou Cnk)

Bon courage

[aviateurpilot]

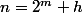
on peux tjrs ecrire avec .

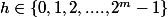
supposons que .
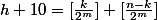
et on a .
donc
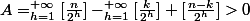
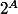
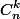
et sais deja que divise qui sera donc pair (absurd).

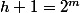
donc et dans ce cas

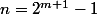
[lapras]

Bravo !
Démonstration tres agréable visuellement, mais plutot difficile a comprendre car elle est tres condensée.
Mais c'est juste !

Autre preuve :
Théoreme de lucas
soit p un nbre premier
n décomposé en base p de facon unique :
n = a0 + a1*p + ... + a_i*p^i
de même
k = b0 + b1*p + ... + b_i*p^i

alors
(n , k) = (a0 , b0)*(a1, b1) * ... * (a_i , b_i) [mod p]
En tenant compte du fait que (n , k) est impair pour TOUT k, on démontre facilement que pour tout i, a_i = 1
donc en base 10
n = 2^(i+1) - 1

[ThSQ]

On peut aussi raisonner modulo 2 :

(a+b)^{2^n} = a^{2^n} + b^{2^n}
....