Ardu problème diophantien.
34 messages
- Page 2 sur 2 - 1, 2
Re: Ardu problème diophantien.
Salut aviateur.
Les 5 valeurs 0,1,2,3,4 à plus petites valeurs réelles (0,11,7,18,14) sont groupées dans le coin haut gauche du tableau. Les 5 cases sont groupées et il n'y a pas d'intrus (un doublon) à l'intérieur.
Il y a un truc simple pour montrer que c'est toujours vrai.
Les 5 valeurs 0,1,2,3,4 à plus petites valeurs réelles (0,11,7,18,14) sont groupées dans le coin haut gauche du tableau. Les 5 cases sont groupées et il n'y a pas d'intrus (un doublon) à l'intérieur.
Il y a un truc simple pour montrer que c'est toujours vrai.
Re: Ardu problème diophantien.
nodgim a écrit:La méthode est perso, et je crois bien qu'elle n'a jamais été établie jusqu'à maintenant. Les matheux étudient davantage les propriétés des relations plutôt que l'usage qu'on peut en faire. Elle est justifiée par une série de propriétés assez intéressantes dont la démo n'est jamais très compliquée.
Bon, ça va j'ai compris
(plus par moi-même que par tes explications que je trouve évasives et qui par conséquent ne justifient rien
 ).
).J'ai amélioré la vitesse de mon algorithme (je suis passé de 60 s à rien du tout pour l'exemple que tu as donné)
Néanmoins je suis curieux sur l'efficacité de ta méthode

Alors je te propose le défi suivant de mettre en oeuvre ta méthode pour
{7057, 16451, 26459}
et pour {7901, 17299, 22621}.
A noter que pour l'un des deux le temps de calcul est environ 4 secondes
Re: Ardu problème diophantien.
Pour l'instant, je n'ai pas dévoilé grand chose de mes explications. Si tu as compris ma démarche, alors fatalement la méthode doit te paraitre justifiée. Si tu trouves qu'elle ne l'est pas, c'est que sans doute tu n'as pas tout vu. As tu trouvé la solution à la connexité ?
Maintenant, pour l'histoire de la rapidité, c'est sûr que l'informatique va aller plus vite (il faut à peu près 1/4 heure, vérification comprise, pour trouver la solution). Mais il s'agissait surtout de montrer qu'il y avait une suite convergente (rapide) qui menait à la solution.
Maintenant, pour l'histoire de la rapidité, c'est sûr que l'informatique va aller plus vite (il faut à peu près 1/4 heure, vérification comprise, pour trouver la solution). Mais il s'agissait surtout de montrer qu'il y avait une suite convergente (rapide) qui menait à la solution.
Re: Ardu problème diophantien.
Bonjour
Evidemment il n' y a rien de connexe dans ton tableau et de mon point de vue tout ça c'est du bluff.
Ce que tu appelles "ta méthode" se trouve dans le papier de Harold Greenberg, Numer. Math. 34, 349-352 (1980) Numerische
Le résultat essentiel étant:le corollaire du th 4 dont je donne l'énoncé ci-dessous.
Corollaire
|L=1,2,...,a_1-1)-a_1)
où=min( a_2x_2+a_3x_3| a_2x_2+a_3x_3 \equiv L mod(a_1)))
et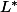 est le nombre cherché (appelé nombre de Frobienus.)
est le nombre cherché (appelé nombre de Frobienus.)
Les valeurs minimales sont évidemment atteintes par les "plus petites valeurs des " et qu'on les retrouve en début de tableau est tout à fait naturel, il n'y a rien a démontré.
" et qu'on les retrouve en début de tableau est tout à fait naturel, il n'y a rien a démontré.
Par contre si on utilise un théorème au moins qu'il soit cité.
Néanmoins merci pour ta question qui me permet de réfléchir dans un domaine que je ne connais pas trop.
Evidemment il n' y a rien de connexe dans ton tableau et de mon point de vue tout ça c'est du bluff.
Ce que tu appelles "ta méthode" se trouve dans le papier de Harold Greenberg, Numer. Math. 34, 349-352 (1980) Numerische
Le résultat essentiel étant:le corollaire du th 4 dont je donne l'énoncé ci-dessous.
Corollaire
où
et
Les valeurs minimales sont évidemment atteintes par les "plus petites valeurs des
Par contre si on utilise un théorème au moins qu'il soit cité.
Néanmoins merci pour ta question qui me permet de réfléchir dans un domaine que je ne connais pas trop.
Re: Ardu problème diophantien.
Pardon Aviateur, mais tu as l'air de penser que j'ai dégotté ça dans une lecture, il n'en est rien. J'ai une très faible culture mathématique, et je préfère nettement m'amuser sur des problèmes plutôt que de lire des mathématiciens (je n'ai d'ailleurs pas le niveau pour les lire, c'est bien trop élevé à mon goût). Du coup, et avec ce que tu viens de trouver (où as tu trouvé cette référence ?) je me rends compte que c'est connu. Tant pis pour moi, mais je me suis bien amusé là dessus.
Maintenant pourquoi dis tu que ce que je trouve connexe ne l'est pas ? Je ne comprends pas.
En tout cas, tu devrais être plus prudent dans tes jugements, je ne sais pas ce que tu entends par "bluff". Le résultat est bluffant, je trouve, mais si le bluff vient, selon toi, du fait que je prends à mon compte un truc que j'ai lu, ben non tu te trompes. Il y a sûrement des gens ici qui me connaissent depuis longtemps, je ne crois pas qu'il me considèrent comme un tricheur.
Donc ce que j'appelle ma méthode est bien ma méthode, je l'ai trouvée tout seul comme un grand.
Sinon, " ma méthode " permet de dire également dans quel cas le plus grand nombre du triplet est inutile.
Enfin, pour le triplet (7057, 16451, 26459 ) je trouve 4 898 683 et pour (7901, 17299, 22621) : 3 546 302
Sauf erreur.
Et bien que les nombres aient un peu monté,c'est pas beaucoup plus long qu'avec des nombres à 3 chiffres.
Maintenant pourquoi dis tu que ce que je trouve connexe ne l'est pas ? Je ne comprends pas.
En tout cas, tu devrais être plus prudent dans tes jugements, je ne sais pas ce que tu entends par "bluff". Le résultat est bluffant, je trouve, mais si le bluff vient, selon toi, du fait que je prends à mon compte un truc que j'ai lu, ben non tu te trompes. Il y a sûrement des gens ici qui me connaissent depuis longtemps, je ne crois pas qu'il me considèrent comme un tricheur.
Donc ce que j'appelle ma méthode est bien ma méthode, je l'ai trouvée tout seul comme un grand.
Sinon, " ma méthode " permet de dire également dans quel cas le plus grand nombre du triplet est inutile.
Enfin, pour le triplet (7057, 16451, 26459 ) je trouve 4 898 683 et pour (7901, 17299, 22621) : 3 546 302
Sauf erreur.
Et bien que les nombres aient un peu monté,c'est pas beaucoup plus long qu'avec des nombres à 3 chiffres.
Re: Ardu problème diophantien.
Bonjour @MMu je me garde bien de prétendre quoi que ce soit concernant le fait que tu as lu ou pas cette méthode quelque part.
A propos de la culture mathématiques on en a tous + ou moins. Concernant la théorie des nombres et au moins pour ce problème je ne peux pas dire que j'ai une culture très grande. Néanmoins avec des raisonnements de base j'arrive à trouver ici la solution. Mais la règle en mathématique, face à un problème, si on apporte une solution c'est de pouvoir la justifier. Quiconque apporte une réponse à un problème doit pouvoir la justifier (i.e l'expliquer) correctement. L'argumentation, la démonstration, ou la preuve sérieuse est le fondement de toute démarche scientifique et en particulier mathématique. Le fait de dire, je suis pas matheux ne justifie pas la validité d'une méthode.
Or il s'avère ici que tu poses un problème et que tu fourni la bonne solution (cela j'en suis sûr car je la trouve à à la suite d'un raisonnement puis avec un calcul avec l'aide d'un algorithme) mais le hic c'est que lorsque je demande comment tu as fait alors les choses ne sont pas claires et cela tu dois l'admettre. D'une part tu appliques une méthode dont tu expliques à peine les calculs et puis on ne voit pas pourquoi à l'arrivée le résultat serait le bon. Je ne mets donc pas en doute ton honnêteté mais je critique simplement ta démarche scientifique. Finalement c'est quoi ta méthode et pourquoi le nombre obtenu est bien le nombre de Frobienus?
Maintenant comme je suis un peu curieux, ayant appris qu'il s'agit du problème de Frobienus, je suis allé voir dans la littérature l'état de la recherche concernant ce problème et je trouve donc l'article (1980) où est justifié la méthode que tu as utilisé.
Concernant les nombres que j'ai donné la réponse c'est bien cela.
A propos de la culture mathématiques on en a tous + ou moins. Concernant la théorie des nombres et au moins pour ce problème je ne peux pas dire que j'ai une culture très grande. Néanmoins avec des raisonnements de base j'arrive à trouver ici la solution. Mais la règle en mathématique, face à un problème, si on apporte une solution c'est de pouvoir la justifier. Quiconque apporte une réponse à un problème doit pouvoir la justifier (i.e l'expliquer) correctement. L'argumentation, la démonstration, ou la preuve sérieuse est le fondement de toute démarche scientifique et en particulier mathématique. Le fait de dire, je suis pas matheux ne justifie pas la validité d'une méthode.
Or il s'avère ici que tu poses un problème et que tu fourni la bonne solution (cela j'en suis sûr car je la trouve à à la suite d'un raisonnement puis avec un calcul avec l'aide d'un algorithme) mais le hic c'est que lorsque je demande comment tu as fait alors les choses ne sont pas claires et cela tu dois l'admettre. D'une part tu appliques une méthode dont tu expliques à peine les calculs et puis on ne voit pas pourquoi à l'arrivée le résultat serait le bon. Je ne mets donc pas en doute ton honnêteté mais je critique simplement ta démarche scientifique. Finalement c'est quoi ta méthode et pourquoi le nombre obtenu est bien le nombre de Frobienus?
Maintenant comme je suis un peu curieux, ayant appris qu'il s'agit du problème de Frobienus, je suis allé voir dans la littérature l'état de la recherche concernant ce problème et je trouve donc l'article (1980) où est justifié la méthode que tu as utilisé.
Concernant les nombres que j'ai donné la réponse c'est bien cela.
Re: Ardu problème diophantien.
Salut Aviateur,
Attention, je suis nodgim, pas MMU, il y a un gros écart de niveau entre nous (pas à mon avantage...).
ça fait un bon moment maintenant que je t'explique que je connais la justification de cette méthode (sinon je ne pourrais pas l'appliquer sans être certain que ça marche à tous les coups ! ) mais que c'est assez long, quoique pas très difficile. Je t'ai dit aussi que si je devais écrire cette justification, faire l'effort de mettre en forme tout ça (ce n'est pas la partie la plus agréable d'une démo), c'est pour que ce soit lu au moins par une personne. Je vais le faire puisque tu es intéressé maintenant et que tu la réclames. Il est vrai que maintenant que tu as découvert que c'était connu, l'intérêt est très limité......
Attention, je suis nodgim, pas MMU, il y a un gros écart de niveau entre nous (pas à mon avantage...).
ça fait un bon moment maintenant que je t'explique que je connais la justification de cette méthode (sinon je ne pourrais pas l'appliquer sans être certain que ça marche à tous les coups ! ) mais que c'est assez long, quoique pas très difficile. Je t'ai dit aussi que si je devais écrire cette justification, faire l'effort de mettre en forme tout ça (ce n'est pas la partie la plus agréable d'une démo), c'est pour que ce soit lu au moins par une personne. Je vais le faire puisque tu es intéressé maintenant et que tu la réclames. Il est vrai que maintenant que tu as découvert que c'était connu, l'intérêt est très limité......
Re: Ardu problème diophantien.
Soit a > b > c et k , j, l entiers naturels. a,b,c premiers > 2.
Problème : quel est le + grand nombre qu'on ne peut pas écrire sous la forme ka + jb + lc ?
Idée : Chercher les c plus petites valeurs réelles de ka+jb telles qu'il n'y a pas 2 valeurs identiques modulo c. La plus grande d'entre elles est le nombre recherché.
On construit un tableau de c*c cases, en 1ère ligne : 0, a, 2a, ....(c-1)a et en 1ère colonne 0, b, 2b,...(c-1)b, Les autres cases étant remplies par l'addition case de 1ère ligne + case de 1ère colonne.
On appelle R(x,y) la valeur réelle dans la case (x,y) et C(x,y) sa valeur modulo c.
Vu qu'il existe c² résultats pour c valeurs modulo c, il y a des doublons.
Soit C(x,y) = C(x+x1, y+y1) avec R(x,y) < R(x+x1,y+y1)
Si C(x,y) = C(x+x1, y+y1) [c] alors pour toute autre case (x',y') : C( x' , y' ) = C(x'+x1, y'+y1) et R(x',y') < R(x'+x1,y'+y1).
Vu la propriété, on peut dire que (x1,y1) est un vecteur recopie. Il existe dans le cas général 3 types de vecteurs recopie, selon le signe de (x1,y1) : VR(+ +), VR(+ -), VR(- +)
Il existe donc R(x'',y'') min telle que R(x>=x''+x1, y>=y"+y1) n'est pas une valeur min car C(x>=x''+x1, y>=y"+y1) est doublon.
Si VR(+,+) : C(x",y") = 0, R(x",y") = 0 et (x",y") = (1,1). De plus C(1, 1+y1) = C(1+x1, 1), autrement dit l'un des multiples de a est le complémentaire [c] de l'un des multiples de b.
Si VR(+,-) : x" = 1 et y"+ y1 = 1, autrement dit l'un des multiples de a est l'égal [c] de l'un des multiples de b.
Si VR(-,+) : y" = 1 et x"+ x1 = 1, autrement dit l'un des multiples de a est l'égal [c] de l'un des multiples de b.
Vu ces règles :
L'espace dans le tableau des c cases contenant les c valeurs recherchées est connexe et convexe (convexe : si (x,y) est l'une de ces cases alors les cases ( <= x, <= y) le sont aussi).
On peut même dire qu'il n'a que 2 formes possibles :
-Un rectangle dans un cas particulier;
-Un rectangle dont l'angle à l'intérieur du tableau est découpé par un rectangle (donc au final une forme en L ou en couloir coudé).
Prouvons tout cela.
Soit minVR(+ -) = VR(+ -) pour x min et minVR(- + ) = VR(- +) pour y min.
minVR(+ -) existe toujours étant donné que a > b. Si c'est VR(1,-), Les c plus petites valeurs sont exclusivement dans la 1ère colonne (puisque la seconde est une recopie de la 1ère). C'est le cas particulier évoqué. Dans ce cas là, le nombre "a" est inutile, et le nombre recherché est classiquement bc-b-c. Et donc minVR(- +) = minVR(++) = VR(0 a)
Si min VR(+,-) = VR(>1, -)
Soit (1,y1) origine de minVR(+ -) et (x1,1) sa fin.
Soit (1,y2) origine de minVR(- +) et (x2,1) sa fin.
Alors on a forcément x2 < x1 et y2 > y1. En effet, si tel n'était pas le cas, VR(x2-x1, y2-y1) ou VR(x1-x2, y2-y1) existe et est < minVR.
Du coup, VR (+ +) existe forcément : VR ( -(x2-x1) (y2-y1) )
Il ne peut pas y avoir 2 VR (++) dans le rectangle délimité par minVR(- + ) et min VR( + -). Si tel était le cas, comme les valeurs [c] dans ces 2 cases supposées sont 0, on créerait immédiatement un VR(+ - ) ou VR (- + ) < min VR.
La recherche des minVR(+ -) minVR(- +) et VR(+ + ) se fait en partant par exemple du 1er multiple de b et du multiple correspondant (même valeur [c] ) de a. La valeur réelle du 1er multiple de b est normalement inférieure au multiple correspondant de a. On cherche alors, en partant du 1er, le plus petit multiple de b qui va être supérieur au multiple de a correspondant. C'est à la transition qu'on trouve le triplet de valeurs recherchées. La valeur max est forcément dans l'une des 2 cases d'angle rentrant de la figure,dont les coordonnées sont données par le triplet trouvé.
Problème : quel est le + grand nombre qu'on ne peut pas écrire sous la forme ka + jb + lc ?
Idée : Chercher les c plus petites valeurs réelles de ka+jb telles qu'il n'y a pas 2 valeurs identiques modulo c. La plus grande d'entre elles est le nombre recherché.
On construit un tableau de c*c cases, en 1ère ligne : 0, a, 2a, ....(c-1)a et en 1ère colonne 0, b, 2b,...(c-1)b, Les autres cases étant remplies par l'addition case de 1ère ligne + case de 1ère colonne.
On appelle R(x,y) la valeur réelle dans la case (x,y) et C(x,y) sa valeur modulo c.
Vu qu'il existe c² résultats pour c valeurs modulo c, il y a des doublons.
Soit C(x,y) = C(x+x1, y+y1) avec R(x,y) < R(x+x1,y+y1)
Si C(x,y) = C(x+x1, y+y1) [c] alors pour toute autre case (x',y') : C( x' , y' ) = C(x'+x1, y'+y1) et R(x',y') < R(x'+x1,y'+y1).
Vu la propriété, on peut dire que (x1,y1) est un vecteur recopie. Il existe dans le cas général 3 types de vecteurs recopie, selon le signe de (x1,y1) : VR(+ +), VR(+ -), VR(- +)
Il existe donc R(x'',y'') min telle que R(x>=x''+x1, y>=y"+y1) n'est pas une valeur min car C(x>=x''+x1, y>=y"+y1) est doublon.
Si VR(+,+) : C(x",y") = 0, R(x",y") = 0 et (x",y") = (1,1). De plus C(1, 1+y1) = C(1+x1, 1), autrement dit l'un des multiples de a est le complémentaire [c] de l'un des multiples de b.
Si VR(+,-) : x" = 1 et y"+ y1 = 1, autrement dit l'un des multiples de a est l'égal [c] de l'un des multiples de b.
Si VR(-,+) : y" = 1 et x"+ x1 = 1, autrement dit l'un des multiples de a est l'égal [c] de l'un des multiples de b.
Vu ces règles :
L'espace dans le tableau des c cases contenant les c valeurs recherchées est connexe et convexe (convexe : si (x,y) est l'une de ces cases alors les cases ( <= x, <= y) le sont aussi).
On peut même dire qu'il n'a que 2 formes possibles :
-Un rectangle dans un cas particulier;
-Un rectangle dont l'angle à l'intérieur du tableau est découpé par un rectangle (donc au final une forme en L ou en couloir coudé).
Prouvons tout cela.
Soit minVR(+ -) = VR(+ -) pour x min et minVR(- + ) = VR(- +) pour y min.
minVR(+ -) existe toujours étant donné que a > b. Si c'est VR(1,-), Les c plus petites valeurs sont exclusivement dans la 1ère colonne (puisque la seconde est une recopie de la 1ère). C'est le cas particulier évoqué. Dans ce cas là, le nombre "a" est inutile, et le nombre recherché est classiquement bc-b-c. Et donc minVR(- +) = minVR(++) = VR(0 a)
Si min VR(+,-) = VR(>1, -)
Soit (1,y1) origine de minVR(+ -) et (x1,1) sa fin.
Soit (1,y2) origine de minVR(- +) et (x2,1) sa fin.
Alors on a forcément x2 < x1 et y2 > y1. En effet, si tel n'était pas le cas, VR(x2-x1, y2-y1) ou VR(x1-x2, y2-y1) existe et est < minVR.
Du coup, VR (+ +) existe forcément : VR ( -(x2-x1) (y2-y1) )
Il ne peut pas y avoir 2 VR (++) dans le rectangle délimité par minVR(- + ) et min VR( + -). Si tel était le cas, comme les valeurs [c] dans ces 2 cases supposées sont 0, on créerait immédiatement un VR(+ - ) ou VR (- + ) < min VR.
La recherche des minVR(+ -) minVR(- +) et VR(+ + ) se fait en partant par exemple du 1er multiple de b et du multiple correspondant (même valeur [c] ) de a. La valeur réelle du 1er multiple de b est normalement inférieure au multiple correspondant de a. On cherche alors, en partant du 1er, le plus petit multiple de b qui va être supérieur au multiple de a correspondant. C'est à la transition qu'on trouve le triplet de valeurs recherchées. La valeur max est forcément dans l'une des 2 cases d'angle rentrant de la figure,dont les coordonnées sont données par le triplet trouvé.
Re: Ardu problème diophantien.
aviateur a écrit:
où
etest le nombre cherché (appelé nombre de Frobienus.)
Est ce que Greenberg détaille la façon d'accéder aux "min" et "max" ?
Re: Ardu problème diophantien.
Bonjour, tu veux dire est-ce qu'il donne un algorithme (plutôt un programme)? la réponse est oui. Mais par contre c'est difficile à comprendre, il faut dire que lire un programme c'est indigeste . Ce que j'ai fait c'est est écrire un algo moi même, il n'est surement pas optimal mais il est meilleur que celui que j'avais déjà fait; évidemment le résultat ici est plus fort que ce que j'avais démontré.
Maintenant visiblement tu utilises le même corollaire (théorème) et visiblement tu arrives au bon résultat.
Pour les exemples j'ai donnés, si tu n'as pas écrit un programme alors c'est là que ça peut être intéressant de comprendre comment tu fais.
Je le répète, il y a deux questionnements que j'ai par rapport à tes réponses
1. C'est quoi exactement ta méthode de calcul?
2. Si tu n'a pas utilisé le théorème que j'ai cité, comment prouve tu que le nombre obtenu est bien le nombre de Frobienus?
Maintenant visiblement tu utilises le même corollaire (théorème) et visiblement tu arrives au bon résultat.
Pour les exemples j'ai donnés, si tu n'as pas écrit un programme alors c'est là que ça peut être intéressant de comprendre comment tu fais.
Je le répète, il y a deux questionnements que j'ai par rapport à tes réponses
1. C'est quoi exactement ta méthode de calcul?
2. Si tu n'a pas utilisé le théorème que j'ai cité, comment prouve tu que le nombre obtenu est bien le nombre de Frobienus?
Re: Ardu problème diophantien.
C'est à dire que pour te répondre précisément, il faudrait que je sache où tu en es dans ce que tu as compris.
Si la forme découpée dans le tableau (ce que j'appelle l'ensemble connexe) est acquise, alors tu es presque au bout du chemin: Il suffit de faire une petite amorce de tableau en plaçant les coordonnées des 3 vecteurs de recopie, le reste n'est que de la lecture.
Le problème est que j'aurais bien aimé mettre un dessin en représentant les vecteurs de recopie qui découpent le tableau, mais bon je suis nul pour ça.
Le vecteur de recopie dirigé de G à D et de B en H découpe la partie verticale du tableau.
Le vecteur de recopie dirigé de D à G et de H en B découpe la partie horizontale du tableau.
Le vecteur de recopie dirigé de G à D et de H en B découpe l'angle du rectangle formé par les 2 vecteurs précédents.
Si la forme découpée dans le tableau (ce que j'appelle l'ensemble connexe) est acquise, alors tu es presque au bout du chemin: Il suffit de faire une petite amorce de tableau en plaçant les coordonnées des 3 vecteurs de recopie, le reste n'est que de la lecture.
Le problème est que j'aurais bien aimé mettre un dessin en représentant les vecteurs de recopie qui découpent le tableau, mais bon je suis nul pour ça.
Le vecteur de recopie dirigé de G à D et de B en H découpe la partie verticale du tableau.
Le vecteur de recopie dirigé de D à G et de H en B découpe la partie horizontale du tableau.
Le vecteur de recopie dirigé de G à D et de H en B découpe l'angle du rectangle formé par les 2 vecteurs précédents.
Re: Ardu problème diophantien.
Attention, il y a peut être un message intercalé que tu n'as pas lu, celui de 6h54.
Re: Ardu problème diophantien.
Rebonjour
@Nogdim
oui je me suis trompé de nom.
non je n'ai pas vu ton message de ce matin.
Je viens de lire avec un peu de mal.
Mais j'ai enfin compris que ce que tu veux dire et en particulier tu utilises une propriété du tableau qui est évidemment facile à montrer (et qui au demeurant est visible sur l'exemple que j'ai donné avec 5, 7 et 11) mais cette propriété est très utile car elle simplifie les calculs.
En résumé, pour faire le lien avec le papier que j'ai cité et d'après moi:
1. Tu utilises le théorème démontré dans le papier mais je ne pense pas que tu le démontres.
2. Tu utilises une propriété simple du tableau et cela n'apparait pas dans le papier en question. Donc ça c'est intéressant.
Ceci étant tout, il y a des algorithmes rapides qui ont été trouvés pour le même travail avec de très grands nombres.
Une remarque: j'ai simplifié l'énoncé du théorème. Mais en fait il reste valable pour n nombres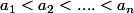 où le plus petit joue toujours le rôle particulier.
où le plus petit joue toujours le rôle particulier.
Il serait intéressant de passer à n=4 (voire plus) et d'écrire l'algorithme de
calcul du nombre de Frobienus en incluant la propriété que tu utilises. Cela ne doit pas être vraiment compliqué il suffit de l'exprimer correctement.
@Nogdim
oui je me suis trompé de nom.
non je n'ai pas vu ton message de ce matin.
Je viens de lire avec un peu de mal.
Mais j'ai enfin compris que ce que tu veux dire et en particulier tu utilises une propriété du tableau qui est évidemment facile à montrer (et qui au demeurant est visible sur l'exemple que j'ai donné avec 5, 7 et 11) mais cette propriété est très utile car elle simplifie les calculs.
En résumé, pour faire le lien avec le papier que j'ai cité et d'après moi:
1. Tu utilises le théorème démontré dans le papier mais je ne pense pas que tu le démontres.
2. Tu utilises une propriété simple du tableau et cela n'apparait pas dans le papier en question. Donc ça c'est intéressant.
Ceci étant tout, il y a des algorithmes rapides qui ont été trouvés pour le même travail avec de très grands nombres.
Une remarque: j'ai simplifié l'énoncé du théorème. Mais en fait il reste valable pour n nombres
Il serait intéressant de passer à n=4 (voire plus) et d'écrire l'algorithme de
calcul du nombre de Frobienus en incluant la propriété que tu utilises. Cela ne doit pas être vraiment compliqué il suffit de l'exprimer correctement.
Re: Ardu problème diophantien.
Pour ce que j'ai fait, ça ne marche qu'avec n=3. Je n'ai pas réfléchi pour n=4.
Si tu as vu des trous dans mon laïus, n'hésite pas surtout, je peux toujours faire des ajouts.
Si tu as vu des trous dans mon laïus, n'hésite pas surtout, je peux toujours faire des ajouts.
34 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 4 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
