Application à déterminer
Olympiades mathématiques, énigmes et défis
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 09 Juil 2007, 10:33
par BiZi » 09 Juil 2007, 10:33
Bonjour!
Un autre petit exo, plus technique celui-là, mais il en faut pour tous les goûts!
Déterminer s'il existe une application f:N*->N* vérifiant:
-f(1)=2
-Pour tout n appartenant à N*, f(f(n))=f(n)+n et f(n)
Question subsidiaire: Comment fait-on N* en Latex? :briques:
-
aviateurpilot
- Membre Irrationnel
- Messages: 1772
- Enregistré le: 01 Juin 2006, 21:33
-
 par aviateurpilot » 09 Juil 2007, 12:18
par aviateurpilot » 09 Juil 2007, 12:18
N* c'est \mathbb{N}^*=
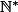
ou N^*=
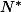
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 09 Juil 2007, 12:51
par Imod » 09 Juil 2007, 12:51
J'ai une solution ( ce n'est sûrement pas la seule ) :
=E(n\varphi+\frac{1}{2}))
.
Avec

: la fonction partie entière et

le nombre d'or .
Imod
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 09 Juil 2007, 13:55
par BiZi » 09 Juil 2007, 13:55
Imod a écrit:J'ai une solution ( ce n'est sûrement pas la seule ) :
=E(n\varphi+\frac{1}{2}))
.
Avec

: la fonction partie entière et

le nombre d'or .
Imod
Bin, ca a l'air de marcher :doh: C'est embêtant, je croyais avoir réussi à démontrer qu'il n'existait pas une telle application :marteau: . Bon, je vais revoir ca. En tout cas, peux-tu détailler un tout petit peu s'il te plaît? Ensuite, je crois qu'on pourra considérer l'exercice comme résolu, vu que l'énoncé n'en demande pas plus :happy2:
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 09 Juil 2007, 14:44
par Imod » 09 Juil 2007, 14:44
Une simple vérification ( j'avais déjà la solution que l'on m'avait sûrement soufflée ) .

est irrationnel ,

et

.
Alors clairement
=2)
et
<f(n+1))
. Il reste à vérifier que
=f(n)+n)
.
=E(n\varphi+\frac{1}{2}))
<n\varphi+\frac{1}{2})
et en divisant par

:
}{\varphi}=f(n)(\varphi-1)<n+\frac{1}{2\varphi}<n+\frac{1}{2})
+n<\varphi f(n)+\frac{1}{2}<f(n)+n+1)
donc
=f(n)+n)
.
Imod
-
BiZi
- Membre Relatif
- Messages: 307
- Enregistré le: 26 Mai 2006, 21:06
-
 par BiZi » 09 Juil 2007, 14:54
par BiZi » 09 Juil 2007, 14:54
Imod a écrit:Une simple vérification ( j'avais déjà la solution que l'on m'avait sûrement soufflée ) .

est irrationnel ,

et

.
Alors clairement
=2)
et
<f(n+1))
. Il reste à vérifier que
=f(n)+n)
.
=E(n\varphi+\frac{1}{2}))
<n\varphi+\frac{1}{2})
et en divisant par

:
}{\varphi}=f(n)(\varphi-1)<n+\frac{1}{2\varphi}<n+\frac{1}{2})
+n<\varphi f(n)+\frac{1}{2}<f(n)+n+1)
donc
=f(n)+n)
.
Imod
Ok c'est bon bravo :happy2:
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 10 Juil 2007, 12:18
par cesar » 10 Juil 2007, 12:18
y a t il d'autres applications qui verifient les conditions de l'énoncé ??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 8 invités
