Algorithme Sympatique:

[FLBP]

Hello,

Lors d'un challenge de prog où on a 2 min pour faire un code qui répond aux contraintes, je suis tombé sur un exo sympa:

Soient deux fonctions :

Code: Tout sélectionner

Fonction foo(n):
--S = 0
--pour 1 <= i <= n:
----si pgdc(i,n) == 1:
------S += 1
--retourne S

et

Code: Tout sélectionner

Fonction bar(N):
--R = 0
--pour 1 <= i <= N:
----si i divise N:
------R += foo(i)
--retourne R

Trouver bar(N) pour N naturel

[LB2]

C'est N mais c'est pas si évident que ça à démontrer!

[FLBP]

Bien vu ! Je laisse la démonstration en énigme

[Ben314]

Salut,
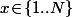
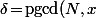Pour fixé, si à tout entier on associe le couple où alors
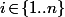
- L'application atterrit dans l'ensemble des couples tels que divise ; et .
- Étant donné un tel couple , il est clair qu'il admet un unique antécédent, à savoir .
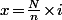
Donc l'application est bijective et ça prouve que

c.q.f.d.