Si on écrit
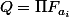
avec
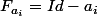
.
Alors, en définissant
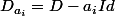
avec

l'opérateur de dérivation sur l'ensemble des fonctions Cinf (par exemple), on obtient :
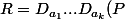)
Maintenant, il faut verifier que pour u réel,
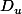
conserve la propriété d'être scindé (ainsi par récurrence, c'est terminé).
En considérant P scindé dans R, de degré n, à k racines distinctes :
On considère
 = P(x)exp{-ux})
Alors
 = 0)
eq
 = 0)
et
 = 0)
eq
(x)=0)
A l'aide du théorème de Rolle, on obtient
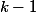
racines simples distinctes de
)
, différentes des racines de

.
Ensuite, en notant
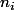
le degré de la racine
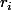
de

, on a que
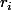
est de degré
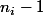
pour
)
.
En sommant les degrés, on obtient bien la somme des
)
- 1, et donc
)
est scindé dans R.
C'est mal dit, et il peut y avoir des erreurs, mais je pense que l'idée de la preuve est là.