soit
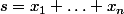
et
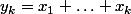
pour k=0...n
alors y0 = 0, et pour tout k = 1 ... n, l'équation numéro k nous dit que
(x1+...+xk)(xk+...+xn) = 1, c'est à dire
 = 1)
donc si par magie on connaît s, on en déduit tous les yk :
y0 = 0, y1 = 1/s, y2 = 1/(s-1/s) = s/(s²-1) etc jusqu'à yn.
si y1,y2,y3... sont positifs et yn = s alors on a gagné.
on regarde donc l'application
 = \frac 1 {s-y})
, qui est un automorphisme de P1(C)
on a les équivalences
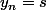
 = s)
 = f_s(s) = \infty)
 = f_s(\infty) = 0)
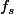
est un automorphisme de P1(C) et normalement ils ont 2 points fixes.
Si un automorphisme a 3 points fixes alors c'est l'identité.
Comme
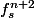
a déjà les 2 points fixes de
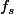
, avoir 0 en plus le force à être l'identité :
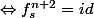
donc on souhaite juste avoir un s qui fait en sorte que
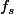
appliqué (n+2) fois, soit l'identité.
Pour étudier les itérés de
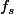
on regarde ce qu'ils font autour des deux points fixes, donc on va regarder leur dérivée en ces points fixes.
Les deux points fixes de
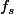
sont solutions de 1 - zs + z² = 0, soit
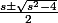
si on veut être précis.
Si s >= 2 alors ils sont réels et donc on a aucune chance d'atteindre s puisque entre 0 et s/2 il y a un point fixe et donc un mur.
Il faut donc regarder le cas 0 < s < 2, où on obtient deux points fixes complexes conjugués
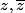
.
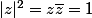
, donc ils sont sur le cercle unité,
et
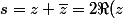)
Maintenant on regarde la dérivée.
 = (s-y)^{-2})
,
et donc
 = (s-z)^{-2} = z^2)
et donc,
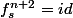
'(z) = 1)
)^{n+2} = 1)
 = exp(\pm 2i \pi/(n+2)))
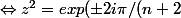))
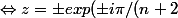))
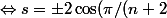))
(en vrai on veut s > 0)
il y a enfin un truc tout à fait magique qui dit que si
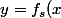)
alors l'angle en z du triangle x y z vaut
)
.
(pour le montrer il faut plutôt parler des cercles passant par x z z', regarder l'angle des tangentes en z, et utiliser le théorème de l'angle au centre enfin ça devient un chouïa compliqué)
donc on trace la droite (0 z), on la tourne de pi/(n+2) autour de z, elle intersecte l'axe des réels en
fs(0) = y1 = x1,
on la tourne encore de pi/(n+2), elle intersecte l'axe des réels en fs(y1) = y2 = x1+x2,
etc etc
et au bout de (n+2) coups on aura tourné la droite de pi, donc on sera revenu à la droite initiale.
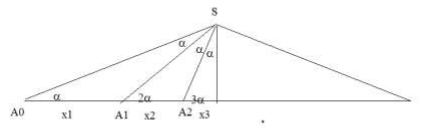
donc on a en effet un beau dessin avec un point z, un bouquet de (n+2) droites dont une horizontale et (n+1) autres qui intersectent une autre droite horizontale en-dessous de z, elles la découpent donc en n segments finis, et les xi sont la longueur de ces segments.
Et les deux segments de droites tout à gauche et tout à droite sont de longueur 1.
A tous les coups y'a un truc du genre thalès ou puissance d'un point par rapport à un cercle qui explique pourquoi le système est résolu en 5 secondes une fois qu'on a le dessin.