Soit un cercle de centre
On a
Je cherche à montrer que:
Malheureusement, j'y arrive pas.
Avez vous une idée s'il vous plaît? Merci d'avance :we: .
Aire et partition
13 messages
- Page 1 sur 1
Aire et partition
par Al-Kashi » 11 Avr 2014, 23:56
Bonjour,
Soit un cercle de centre
et de rayon 
. Voir la figure ici.
On a
.
Je cherche à montrer que:
+aire(GAE)+aire(IAB)+aire(CAH)=2\theta)
Malheureusement, j'y arrive pas.
Avez vous une idée s'il vous plaît? Merci d'avance :we: .
Soit un cercle de centre
On a
Je cherche à montrer que:
Malheureusement, j'y arrive pas.
Avez vous une idée s'il vous plaît? Merci d'avance :we: .
par Ben314 » 12 Avr 2014, 00:17
Salut,
Les droites (BC) et (DE) sont perpendiculaires ?
Les droites (BC) et (DE) sont perpendiculaires ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Al-Kashi » 12 Avr 2014, 00:47
Ben314 a écrit:Salut,
Les droites (BC) et (DE) sont perpendiculaires ?
Oui les droites (BC) et (DE) sont perpendiculaires.
par Al-Kashi » 12 Avr 2014, 00:53
Désolé, j'ai posté en double ! Est-ce qu'il est possible de supprimer ce message ?
par Imod » 12 Avr 2014, 07:47
C'est le fameux théorème de la pizza , une petite recherche sur la toile devrait te donner plein de réponses .
Imod
Imod
par Al-Kashi » 12 Avr 2014, 12:38
Imod a écrit:C'est le fameux théorème de la pizza , une petite recherche sur la toile devrait te donner plein de réponses .
Imod
Bonjour,
Merci bcp pour ta réponse. Je ne connaissais pas ce théorème -:). On apprend tous les jours sur le forum.
Très bonne journée.
par Ben314 » 13 Avr 2014, 12:03
En fait, ce n'est pas super compliqué à montrer :
Tu prend un point
sur le cercle, tu note 
l'angle )
et )
la longueur 
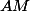
qui s'exprime simplement en utilisant Al-Kashi dans OAM :
=d\cos\alpha +\sqrt{R^2-d^2\sin^2\alpha}\)
où 
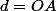
et 
rayon du cercle.
La surface du secteur FAD (par exemple) est alors 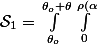}\rho\,d\rho d\alpha=\frac{1}{2}\int_{\theta_o}^{\theta_o+ \theta }\rho^2(\alpha) d\alpha)
.
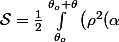Donc la surface des 4 secteurs est+\rho^2(\alpha+\frac{\pi}{2})+\rho^2(\alpha+\pi)+\rho^2(\alpha+\frac{3\pi}{2}) \big)d\alpha)
.
Et on vérifie aisément que+\rho^2(\alpha+\frac{\pi}{2})+\rho^2(\alpha+\pi)+\rho^2(\alpha+\frac{3\pi}{2})=4R^2)
.
Donc
qui ne dépend ni de 
, ni de 
.
Et on doit façilement pouvoir pas mal généraliser vu que, déjà,
+\rho^2(\alpha+\pi)=2\big(R^2+ d^2 \cos (2\alpha)\big))
est extrêmement simple.
Tu prend un point
La surface du secteur FAD (par exemple) est alors
Donc la surface des 4 secteurs est
Et on vérifie aisément que
Donc
Et on doit façilement pouvoir pas mal généraliser vu que, déjà,
est extrêmement simple.
Modifié en dernier par Ben314 le 12 Fév 2017, 01:00, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Imod » 13 Avr 2014, 16:57
@Ben
En fait c'est bien plus simple que ça , on peut obtenir le résultat avec un peu de géométrie élémentaire .
Imod
En fait c'est bien plus simple que ça , on peut obtenir le résultat avec un peu de géométrie élémentaire .
Imod
par Ben314 » 13 Avr 2014, 17:39
Imod a écrit:@Ben
En fait c'est bien plus simple que ça , on peut obtenir le résultat avec un peu de géométrie élémentaire .
Imod
Tu as une référence ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Ben314 » 13 Avr 2014, 22:23
Merçi, mais dans l'article en question, il me semble qu'ils parlent principalement (exclusivement ?) de découpages avec des angles en A égaux (à Pi/N) alors que ce n'est pas le cas içi (où alors il y a une astuce qui m'a échappé... 
)
C'est en partant du dessin de la page 424 qu'on en déduit facilement le cas exposé par Al-Kashi dans son Post (est dans lequel thêta est un angle quelconque) ?
)C'est en partant du dessin de la page 424 qu'on en déduit facilement le cas exposé par Al-Kashi dans son Post (est dans lequel thêta est un angle quelconque) ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
par Imod » 14 Avr 2014, 14:44
Oui c'est vrai , j'avais lu la question un peu vite et comme sur le dessin tous les angles font 45° ...
Imod
Imod
par Al-Kashi » 15 Avr 2014, 21:18
Merci à vous Ben314 et Imod :lol3:, j'ai réussi à faire le calcul.
A très bientôt
A très bientôt
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 7 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :