Aidez-moi à résoudre ce problème!!

[mln]

Il me semblait que 0 était à la fois pair et impair: en effet 0=2k*0 pour k€Z et 0=(2k+1)*0 pour k€Z. Dans ce cas on peut l'utiliser. dites si j'ai dit une grosse bêtise

un entier relatif n est pair si il existe un entier relatif k tel que n=2k.
un entier relatif n est impair si il existe un entier relatif k tel que n=2k+1.
( si n=(2k+1)x, la parité de n est la meme que la parité de x)

0=2*0 donc 0 est pair.

Il n'existe pas de solution à ce problème dans Z Comme beaucoup l'ont montré.


une "solution" vraiment tirée par les cheveux: raisonner dans Z/9Z par exemple:

cependant peut-on encore parler d'entiers impairs?

[aviateurpilot]

salut
quand on dit soit b un nombre de N et qu'on dois trouver ca valeur sachant quel verifie quelque equation par exmple b+1=10
tt le mondre va trouve que b=9
alors ici. on vois que tt le monde va travailler dans la base 10
mais si on travaille dans la base 7 on va trouver que b=6
là on a 6 pair et 1 impair mais 6+1=10 pair

[aviateurpilot]

la solution de x+1=10 dans la base 7 et x=6
meme si x dois etre impair car 1 impair et 10 pair

[Quidam]

mea culpa pour ma solution.

Pas de soucis.

ceci dit si je reprends ma proposition 7^3+7^2+7^1+1 est impair en base 7 et pair en base 10. IL en est de même de 40 qui s'écrit 1111 en base 3

... mais tu recommences ! Etre impair, ne signifie pas "se terminer par un chiffre impair" !

Néanmoins, je pense que la notion de parité n'a plus de sens lorsqu'on ne se place plus en base 10

Tu fais erreur, la parité n'a rien à voir avec la base ! Etre pair, c'est être divisible par 2, être impair, c'est ne pas l'être ! Si la base est paire, la parité du dernier chiffre est la même que la parité du nombre ; si la base est impaire, on ne peut rien conclure sur la parité du nombre à partir de la parité du dernier chiffre !

[murray]

1111 est-il divisible par 2 en base 3 ?

[Quidam]

1111 est-il divisible par 2 en base 3 ?

Je dirais que le nombre qui est représenté par est bien sûr égal à et est bien sûr divisible par 2 :


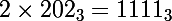
Puisque :

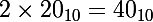
[Patastronch]

1111 est-il divisible par 2 en base 3 ?

j'aprouve, depuis quand la parité ne dépends que de la parité des chiffres qui terminent le nombre ? C'est une propriété de la base 10 (des bases pairs meme) le fait que le dernier chiffre doive etre pair pour que le nombre soit pair.