Aide: Formule à calculer

par **washwash** » 22 Avr 2017, 12:20

Soient

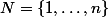
, et

, avec

.
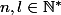
Je cherche à calculer cette formule:

où,

, et

,

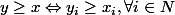
Merci par avance

par **washwash** » 22 Avr 2017, 15:03

Exemple: n=1

par **washwash** » 22 Avr 2017, 20:40

Est ce que c'est possible le calcule ou non ?
Merci par avance

par **Pseuda** » 23 Avr 2017, 06:46

Bonjour,

Pour ceux qui voudront répondre, peux-tu expliquer déjà ce qu'est : |A(x)|, module d'un ensemble ?

par **washwash** » 23 Avr 2017, 08:16

est le cardinal de l'ensemble

.
Exemple, si

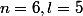
, et

,
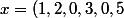alors,

, et

.

par **Pseuda** » 23 Avr 2017, 08:48

Ok ! Je n'y avais pas pensé.

par **washwash** » 23 Avr 2017, 10:50

Je pense que c'est impossible de faire le calcul, c'est inexploitable ?