soit a ,b et c des entiers strictement positifs tels que :
a/b+b/c+c/a est un entier
montrer que abc est un cube.
merci
Abc
11 messages
- Page 1 sur 1
On note k l'entier a/b+b/c+c/a
Soit d le PGCD de a,b,c. On pose a=da', b=db' et c=dc'.
a'/b'+b'/c'+c'/a' est aussi égal à k et si on montre que a'b'c' est le cube d'un entier x, on aura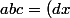^3) .
.
En résumé, on peut supposer a, b, c, premiers entre eux (dans leur ensemble).
On a alors a²c+b²a+c²b=kabc. (1)
Soit p un diviseur premier de abc. On peut supposer par exemple que p|a. On pose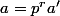 avec a' étranger à p.
avec a' étranger à p.
D'après (1) , p|b²c, donc p divise b ou c (mais pas les deux).
Premier cas : p|b
On pose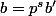 avec b' étranger à p.
avec b' étranger à p.
On reporte dans l'égalité (1) :
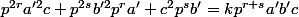 . (2)
. (2)
On voit que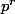 divise le second membre et les deux premiers termes du premier membre, donc il divise aussi
divise le second membre et les deux premiers termes du premier membre, donc il divise aussi 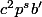 , c'est à dire que
, c'est à dire que 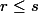 . On peut simplifier (2) par
. On peut simplifier (2) par 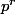 :
:
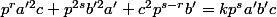 .
.
A nouveau, on a trois termes sur 4 multiples de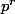 donc le quatrième l'est aussi. On simplifie :
donc le quatrième l'est aussi. On simplifie :
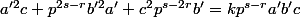 .
.
Le premier terme n'est pas multiple de p et donc au moins un des trois autres termes non plus : ce ne peut être que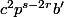 (celui de valuation p-adique minimale). D'où 2r=s.
(celui de valuation p-adique minimale). D'où 2r=s.
Ainsi la valuation p-adique de abc est 3r.
Deuxième cas : p|c. se fait de manière analogue.
On a donc prouvé que tout diviseur premier de abc est de valuation multiple de 3 dans abc. Cela prouve bien que abc est un cube.
Soit d le PGCD de a,b,c. On pose a=da', b=db' et c=dc'.
a'/b'+b'/c'+c'/a' est aussi égal à k et si on montre que a'b'c' est le cube d'un entier x, on aura
En résumé, on peut supposer a, b, c, premiers entre eux (dans leur ensemble).
On a alors a²c+b²a+c²b=kabc. (1)
Soit p un diviseur premier de abc. On peut supposer par exemple que p|a. On pose
D'après (1) , p|b²c, donc p divise b ou c (mais pas les deux).
Premier cas : p|b
On pose
On reporte dans l'égalité (1) :
On voit que
A nouveau, on a trois termes sur 4 multiples de
Le premier terme n'est pas multiple de p et donc au moins un des trois autres termes non plus : ce ne peut être que
Ainsi la valuation p-adique de abc est 3r.
Deuxième cas : p|c. se fait de manière analogue.
On a donc prouvé que tout diviseur premier de abc est de valuation multiple de 3 dans abc. Cela prouve bien que abc est un cube.
Soit p un nombre premier,et a',b' et c' les valuations p-adiques
de a, b et c. On veut montrer que a'+b'+c' est un multiple de 3.
on a (a'-b')+(b'-c')+(c'-a')= 0
Il en résulte que lun au moins des trois entiers a'-b',b'-c' et c'-a' est négatif. Si aucun
nest strictement négatif, cest que a'=b'=c' et a'+b'+c' est bien muliple de 3. Sinon, pour que) >ou =0 ,le minimum des trois valeurs doit étre atteint au moins deux fois. Par
>ou =0 ,le minimum des trois valeurs doit étre atteint au moins deux fois. Par
exemple, on a a'-b'=b'-c', ce qui assure que a'+b'+c'=3b' est encore multiple de 3.
donc si p divise abc) est divisible par 3
est divisible par 3
donc abc est un cube
de a, b et c. On veut montrer que a'+b'+c' est un multiple de 3.
on a (a'-b')+(b'-c')+(c'-a')= 0
Il en résulte que lun au moins des trois entiers a'-b',b'-c' et c'-a' est négatif. Si aucun
nest strictement négatif, cest que a'=b'=c' et a'+b'+c' est bien muliple de 3. Sinon, pour que
exemple, on a a'-b'=b'-c', ce qui assure que a'+b'+c'=3b' est encore multiple de 3.
donc si p divise abc
donc abc est un cube
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 9 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
