0!=1
"Dr James Grime tries to explain why this is the case"
=>
https://www.youtube.com/watch?v=Mfk_L4Nx2ZI
Zero Factorial - Numberphile
6 messages
- Page 1 sur 1
... en fait la seule explication valide est celle -ci (tout autre explication étant à rejeter ipso facto) :
le nombre de bijections d'un ensemble vide dans lui même est 0!=1 avec 0 est le cardinal de l'ensemble vide
pour démontrer ensuite qu'il existe bien une bijection d'un ensemble vide dans lui même on pose la démo ainsi
d'un ensemble vide dans lui même on pose la démo ainsi
il suffit de démontrer qu'il existe bien une application d'un ensemble vide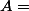 dans un ensemble quelconque
dans un ensemble quelconque  (donc pouvant lui aussi être vide)
(donc pouvant lui aussi être vide)
puis de démontrer que cette application est à la fois une surjection et une injection
cette application existe et celle ci est unique car elle correspond au graphe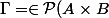)
où) désigne l'ensemble de toutes les parties de
désigne l'ensemble de toutes les parties de 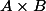
effectivement dans ce cas le domaine de définition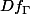 du graphe
du graphe 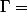 est
est
\in \Gamma \}=\empty)
or pour qu'une application entre deux ensembles et
et  existe il faut que cette correspondance de
existe il faut que cette correspondance de  vers
vers  possède un graphe
possède un graphe  qui soit fonctionnel et tel que de plus
qui soit fonctionnel et tel que de plus  soit le domaine de définition de ce graphe ce qui est le cas ici car on vérifie
soit le domaine de définition de ce graphe ce qui est le cas ici car on vérifie
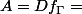
où la correspondance se définit par un triplet)
par ailleurs ce graphe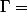 est effectivement fonctionnel car pour qu'un graphe
est effectivement fonctionnel car pour qu'un graphe  de
de  vers
vers  soit fonctionnel il faut et il suffit que
soit fonctionnel il faut et il suffit que 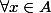
soit uniquement que\in \Gamma \}=\empty) ce qui est le cas ici car
ce qui est le cas ici car 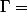 et que par conséquent il n'existe pas d'élément
et que par conséquent il n'existe pas d'élément \in \Gamma)
soit uniquement que\in \Gamma \}) est un singleton
est un singleton
on demontre que cette application est une injection effectivement (selon
est une injection effectivement (selon 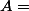 ) on vérifie bien
) on vérifie bien \in A\times A) on obtiens bien l'implication logique
on obtiens bien l'implication logique =b(y))\Rightarrow (x=y)) qui reste vrai
qui reste vrai
cette application est aussi une surjection car l'ensemble d'application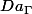 du graphe
du graphe 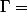 est l'ensemble
est l'ensemble 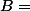 en effet ici
en effet ici
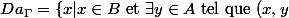\in \Gamma \}=\empty)
le nombre de bijections d'un ensemble vide dans lui même est 0!=1 avec 0 est le cardinal de l'ensemble vide
pour démontrer ensuite qu'il existe bien une bijection
il suffit de démontrer qu'il existe bien une application d'un ensemble vide
puis de démontrer que cette application est à la fois une surjection et une injection
cette application existe et celle ci est unique car elle correspond au graphe
où
effectivement dans ce cas le domaine de définition
or pour qu'une application entre deux ensembles
où la correspondance se définit par un triplet
par ailleurs ce graphe
soit uniquement que
soit uniquement que
on demontre que cette application
cette application est aussi une surjection car l'ensemble d'application
,messinmaisoui a écrit:C'est la rubrique détente ici :doh: ...
oui pardon camarade Messinmaisoui , bon alors pour rattraper ce que j'ai dit ...je profite de ma pause de 10 heures pour laisser les pataphysiciens parler (je parle des vrais ... pas des débutants comme moi)
la pataphysique n'étant pas une science je corrige mon post par ce lien là en rubrique détente
(ceci dit faudra m'expliquer en quoi ce lien là ci-dessous détend ...par contre le rapport avec ce fil-ci est évident car le volcan stipulant que 0! = 1 ne fait pas de cadeau ... et même il tue )
https://www.youtube.com/watch?v=WyVxpgMHwuE
...merci pour eux camarade
n'oublions pas (non jamais) les maitres de la pataphysique
bon pour se rappeler que effectivement 0!=1 et comme en echoe de la catastrophe jadis du volcan en colère des démonstrations falsifiées de cette vérité qui crie à travers les âges et depuis des milliards de milliards d'années (oui des milliards de milliards d'années)
un echoe venu d'ailleurs https://www.youtube.com/watch?v=bnC7TdkRnP4
n'oublions pas (non jamais) les maitres de la pataphysique
bon pour se rappeler que effectivement 0!=1 et comme en echoe de la catastrophe jadis du volcan en colère des démonstrations falsifiées de cette vérité qui crie à travers les âges et depuis des milliards de milliards d'années (oui des milliards de milliards d'années)
un echoe venu d'ailleurs https://www.youtube.com/watch?v=bnC7TdkRnP4
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 3 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
