Quel âge ai-je ?
Venez à la rencontre des autres membres: discussions en tous genres (sauf politiques), anniversaires, faits divers
-
Hartséne
- Messages: 2
- Enregistré le: 30 Oct 2012, 12:32
-
 par Hartséne » 30 Oct 2012, 12:35
par Hartséne » 30 Oct 2012, 12:35
Mon âge :

Quel est-il ?
(A vrai dire, c'est pour vérifier que j'ai bien calculé...)
-
SaintAmand
- Membre Rationnel
- Messages: 901
- Enregistré le: 17 Oct 2011, 11:47
-
 par SaintAmand » 30 Oct 2012, 13:35
par SaintAmand » 30 Oct 2012, 13:35
Comment définies-tu
\,\mathrm{d}x)
avec

,
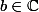
?
-
Hartséne
- Messages: 2
- Enregistré le: 30 Oct 2012, 12:32
-
 par Hartséne » 30 Oct 2012, 15:15
par Hartséne » 30 Oct 2012, 15:15
Justement, c'est ce qui m'étonne, mais ça n'a pas l'air de poser problème à Maple, et je ne trouve pas de réponse qui me satisfasse sur Internet : qu'en est-il, selon vous ?
-
Deliantha
- Membre Relatif
- Messages: 352
- Enregistré le: 05 Juil 2012, 12:09
-
 par Deliantha » 30 Oct 2012, 18:15
par Deliantha » 30 Oct 2012, 18:15
Hartséne a écrit:Justement, c'est ce qui m'étonne, mais ça n'a pas l'air de poser problème à Maple, et je ne trouve pas de réponse qui me satisfasse sur Internet : qu'en est-il, selon vous ?
Cette formule copiée n'empêche pas de faire fi du h et d'avoir déjà en tête la primitive de
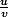
.
En vie réelle, l'humour ne dispense pas de cultiver des idées et d'arriver à les exprimer en H.S. :ptdr:
-
Deliantha
- Membre Relatif
- Messages: 352
- Enregistré le: 05 Juil 2012, 12:09
-
 par Deliantha » 31 Oct 2012, 18:26
par Deliantha » 31 Oct 2012, 18:26
Cette formule en un est celle de l'âge d'un des miens aujourd'hui
^h}}{ln(h+1)}* \frac{10}{17} * {\bigint_{1}^{e^{\frac{4 \pi}{h}} }\frac{x^{h-1}}{x^h + h -4}dx]_{h=4})
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 2 invités
