Vecteurs
Réponses à toutes vos questions du CP à la 3ème
-
roumy_57
- Membre Naturel
- Messages: 27
- Enregistré le: 03 Jan 2007, 13:52
-
 par roumy_57 » 11 Avr 2007, 12:27
par roumy_57 » 11 Avr 2007, 12:27
Bonjour, j'ai un petit exercice a faire pour la rentrée, j'ai tout fait mis à part la dernière question!
Soit (O,I, J) un repère orthonormal du plan (unité le cm).
a) Placer les points A(-1;2) , B(3;4) et C(2;-4).
b) Calculer les distances AB, AC et BC. [AB= 4,5cm, AC= 6,7cm et BC= 7,3cm]
c) Démontrer que le triangle ABC est rectangle. [Il n'est pas rectangle]
d) Calculer les coordonnées du milieu M par la translation de vecteur BC. [ J'ai trouvée M(1;3) ]
e) Construire le point N, image de M par la translation de vecteur BC.
f) Démontrer que (MN) coupe [AC] en son milieu. [Je n'arrive pas a résoudre cette question]
Pourriez-vous m'aider?
Merci d'avance.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 11 Avr 2007, 12:37
par Flodelarab » 11 Avr 2007, 12:37
On te demande pas de déterminer s'il est rectangle ... on te demande de prouver qu'il l'est
donc tu t'es trompé.
-
roumy_57
- Membre Naturel
- Messages: 27
- Enregistré le: 03 Jan 2007, 13:52
-
 par roumy_57 » 11 Avr 2007, 13:16
par roumy_57 » 11 Avr 2007, 13:16
Ah, mais je vois pas où je me suis trompé.
-
oscar
- Membre Légendaire
- Messages: 10024
- Enregistré le: 17 Fév 2007, 20:58
-
 par oscar » 11 Avr 2007, 13:17
par oscar » 11 Avr 2007, 13:17
Bonjour
DONNEES A(-1;2) B(3;4)C(2;-4)
Recherche
1) Distance Ac²=9+36 =45
Distance Ab²=16-4 = 20
Distance BC²=1+64=65
65=45+20=>ectangle en A
2)Je ne trouve pas M ni N
Indique le pour continuer :!:
-
roumy_57
- Membre Naturel
- Messages: 27
- Enregistré le: 03 Jan 2007, 13:52
-
 par roumy_57 » 11 Avr 2007, 13:48
par roumy_57 » 11 Avr 2007, 13:48
Oscar,
Pour le 1) j'ai trouvé BC²=53.
Je ne comprends pas comment tu as trouvé 65.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 11 Avr 2007, 13:54
par Flodelarab » 11 Avr 2007, 13:54
roumy_57 a écrit:Oscar,
Pour le 1) j'ai trouvé BC²=53.
Je ne comprends pas comment tu as trouvé 65.
Ben .... il l'a pourtant écrit.
Donne nous ton calcul Roumy. On te diras ou c pas bon
-
roumy_57
- Membre Naturel
- Messages: 27
- Enregistré le: 03 Jan 2007, 13:52
-
 par roumy_57 » 11 Avr 2007, 13:59
par roumy_57 » 11 Avr 2007, 13:59
Non finalement, j'ai bien refais le calcul, j'ai trouvé 65.
J'avais fait une erreur de calcul.
-
roumy_57
- Membre Naturel
- Messages: 27
- Enregistré le: 03 Jan 2007, 13:52
-
 par roumy_57 » 11 Avr 2007, 14:07
par roumy_57 » 11 Avr 2007, 14:07
Il manque une question:
F) Calculer les coordonnées de N.
G) Démontrer que (MN) coupe [AC] en son milieu.
-
roumy_57
- Membre Naturel
- Messages: 27
- Enregistré le: 03 Jan 2007, 13:52
-
 par roumy_57 » 11 Avr 2007, 14:15
par roumy_57 » 11 Avr 2007, 14:15
Pour la f) j'ai trouvé que N(2;11)
Es-ce juste?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 11 Avr 2007, 14:26
par Flodelarab » 11 Avr 2007, 14:26
roumy_57 a écrit:Pour la f) j'ai trouvé que N(2;11)
Es-ce juste?
non c faux.
same player shoot again
-
roumy_57
- Membre Naturel
- Messages: 27
- Enregistré le: 03 Jan 2007, 13:52
-
 par roumy_57 » 11 Avr 2007, 14:59
par roumy_57 » 11 Avr 2007, 14:59
Ok pourquoi alors?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 11 Avr 2007, 15:06
par Flodelarab » 11 Avr 2007, 15:06
roumy_57 a écrit:Ok pourquoi alors?
si tu ne me montres pas tes calculs, je ne peux pas dire.
la faute est purement calculatoire je pense. Rien de grave
-
roumy_57
- Membre Naturel
- Messages: 27
- Enregistré le: 03 Jan 2007, 13:52
-
 par roumy_57 » 11 Avr 2007, 18:14
par roumy_57 » 11 Avr 2007, 18:14
J'ai écris:
f)MBCN étant un parallélogramme vect MN= vectBC.
vectBC(2-3;-4-4) = vectBC(-1:-8)
vectBC=vectMN
vectBC(-1;-8)=vectMN(1-xn;3-yn)
-1=1-xn
-8=3-yn
-1-1=-xn
-8-3=-yn
-2=-xn
-11=-yn
2=xn
11=yn
N(2;11)
Voilà mes calculs
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 11 Avr 2007, 19:08
par Flodelarab » 11 Avr 2007, 19:08
La faute vient du fait que tu as calculé les coordonnées de
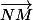
et non
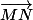
-
roumy_57
- Membre Naturel
- Messages: 27
- Enregistré le: 03 Jan 2007, 13:52
-
 par roumy_57 » 11 Avr 2007, 19:45
par roumy_57 » 11 Avr 2007, 19:45
Explique-moi stp, je comprends pas là.
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 11 Avr 2007, 22:00
par Flodelarab » 11 Avr 2007, 22:00
Flodelarab a écrit:La faute vient du fait que tu as calculé les coordonnées de
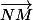
et non
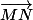
tu as calculé
)
et il faut calculer
)
-
roumy_57
- Membre Naturel
- Messages: 27
- Enregistré le: 03 Jan 2007, 13:52
-
 par roumy_57 » 12 Avr 2007, 11:42
par roumy_57 » 12 Avr 2007, 11:42
Ah d'accord, j'ai éssayé, j'ai trouvé:
vectBC(-1;-8) = vectMN(xn-1;yn-3)
-1=xn-1
-8=yn-3
-1+1=xn
-8+3=yn
0=xn
-5=yn
N(0;-5)
Pour la question g) Démontrer que (MN) coupe [AC] en son milieu, je dois calculer le milieu de [AC]?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 12 Avr 2007, 14:10
par Flodelarab » 12 Avr 2007, 14:10
roumy_57 a écrit:Pour la question g) Démontrer que (MN) coupe [AC] en son milieu, je dois calculer le milieu de [AC]?
J'voue que cette question me laisse perplexe. On ne comprend pas s'il s'agit du cas particulier ou si la démonstration doit etre faite pour TOUT triangle....
A ta place, je traiterais le cas particulier. Donc, oui, je calculerais le milieu de AC et je montrerais qu'il est sur [MN]
-
rene38
- Membre Légendaire
- Messages: 7135
- Enregistré le: 01 Mai 2005, 11:00
-
 par rene38 » 12 Avr 2007, 14:41
par rene38 » 12 Avr 2007, 14:41
Bonjour
Et pourquoi pas la "droite des milieux" dans le triangle ABC ?
-
roumy_57
- Membre Naturel
- Messages: 27
- Enregistré le: 03 Jan 2007, 13:52
-
 par roumy_57 » 12 Avr 2007, 16:46
par roumy_57 » 12 Avr 2007, 16:46
Donc je pourrais tout simplement écrire:
Dans le triangle rectangle ABC, la droite (MN) passe par le milieu de [AB] et est parallèle à [BC] alors elle passe par le milieu de [AC].
Donc (MN) coupe [AC] en son milieu.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 16 invités
