Bonjour,
J’ai un dm en maths. Je ne comprends pas comment faut-il faire des raisonnements ( par l’absurde, par récurrence…). Pouvez vous me citer quels sont les autres types de raisonnements s’il vous plaît et de m’expliquer aussi l’exercice.
Voici le sujet:
Soit une fonction f définie sur une intervalle I et deux nombres distincts a et b appartenant à I.
1-Montrer que, si f est croissante sur I, alors le taux de variation sur f entre a et b est positif.
2-De façon analogue, montrer que, si f est décroissante sur I, alors le taux de variation de f entre a et b est négatif.
Montrer une implication:
Une implication est une propriété qui s’écrit: P->Q
Cela signifie: si P est vraie, alors Q est vraie.
Merci pour votre aide
Utiliser différents raisonnements maths
9 messages
- Page 1 sur 1
Re: utiliser différents raisonnements maths
Bonjour
Quelle définition avez vous pour "f est croissante sur I " ?
Quelle définition pour "taux de variation de f sur I "?
Quelle définition avez vous pour "f est croissante sur I " ?
Quelle définition pour "taux de variation de f sur I "?
Re: utiliser différents raisonnements maths
Le taux de variation est définie sur f(b)-f(a)/b-a
et
Si f est croissante sur I et bien on a f’(x)<ou égale à 0
Est-ce bien ça ?
et
Si f est croissante sur I et bien on a f’(x)<ou égale à 0
Est-ce bien ça ?
Re: utiliser différents raisonnements maths
Non
f est croissante sur si et seulement si
Quels que soient a et b éléments de I, si a<b alors f(a)<=f(b)
Taux de variation sur I :
-f(b)}{a-b}) où a et b sont deux éléments distincts de I
où a et b sont deux éléments distincts de I
f est croissante sur si et seulement si
Quels que soient a et b éléments de I, si a<b alors f(a)<=f(b)
Taux de variation sur I :
Re: utiliser différents raisonnements maths
Donc après je dois faire pareil pour la deuxième question c’est bien ça ?
Re: utiliser différents raisonnements maths
Pouvez-vous m’expliquer quels raisonnements faut-il utiliser et comment s’il vous plaît
Re: utiliser différents raisonnements maths
bonsoir,
a,b deux réels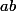
-f(a)}{b-a}=\dfrac{f(a)-f(b)}{a-b})
sans perte de généralité, on peut supposer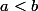 (sinon, on permute a et b)
(sinon, on permute a et b)
comme f est strictement décroissante,>f(b)) donc
donc -f(a) <0)
or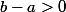 d'où
d'où -f(a)}{b-a}<0)
a,b deux réels
sans perte de généralité, on peut supposer
comme f est strictement décroissante,
or
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 17 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
