[3ème+] Une simplification

[benekire2]

Bonjour, je propose un petit exo assez marrant aux collégiens :

Simplifier

Bon travail

Edit: Bon, cela dit on a peut être besoin d'un ou deux résultats de seconde ...

[Lostounet]

Salut!
Des indices? Je ne vois pas trop O_o
J'arrive à des racines "sixièmes", des racines quadratiques...?

Merci :D

[benekire2]

Salut Lostounet !

Rien de tout ça ,

Commence par factoriser a^3+b^3 et regarde ce que tu peut en faire ...

[Lostounet]

On va dire que a³ + b³ = (a-b)(a²+ab+b²) ?

[ffpower]

ca ressemble a des formules de Cardan, mais t es sur que la deuxieme racine n est pas une racine cubique?

[benekire2]

Plutôt a^3+b^3=(a+b)(a²-ab+b²) et tu peut développer pour vérifier. Maintenant on peut "améliorer" ce que je vient de te donner , et l'exprimer qu'avec des (a+b) [ce que l'on cherche] et des ab , ce qui est relativement simple a calculer ... de plus a^3+b^3 est aussi facile a calculer.

On va donc trouver une équation d'inconnue X=(a+b) ....

[benekire2]

ca ressemble a des formules de Cardan, mais t es sur que la deuxieme racine n est pas une racine cubique?

Si si effectivement, c'en est une de racine cubique et non carré.

J'ai donné toutes les indications pour lostounet. Pas d'autres :zen: !
( Je rigole bien entendu, t'en aura tant que tu demandera .. )

Par contre la solution en blanqué :

On remarque que a^3+b^3=(a+b)(a²-ab+b²)=(a+b)((a+b)²-3ab)
or ici a^3+b^3=90 et ab=7 d'où 90=(a+b)((a+b)²-21) i.e avec X=(a+b) on a X^3-21X-90=0 or 6 est solution "évidente" on peut donc réécrire : (X-6)(X²+6X+15)=0
Or X²+6X+15=X²+6X+9+6=(X+3)²+6>0 d'où X^3-21X-90=0 X=6 et on en déduit que ce truc horrible vaut en fait 6.


Voilà :++:

[Sve@r]

Si si effectivement, c'en est une de racine cubique et non carré.

J'ai donné toutes les indications pour lostounet. Pas d'autres :zen: !
( Je rigole bien entendu, t'en aura tant que tu demandera .. )

Par contre la solution en blanqué :
On remarque que a^3+b^3=(a+b)(a²-ab+b²)=(a+b)((a+b)²-3ab)
or ici a^3+b^3=90 et ab=7 d'où 90=(a+b)((a+b)²-21) i.e avec X=(a+b) on a X^3-21X-90=0 or 6 est solution "évidente" on peut donc réécrire : (X-6)(X²+6X+15)=0
Or X²+6X+15=X²+6X+9+6=(X+3)²+6>0 d'où X^3-21X-90=0 X=6 et on en déduit que ce truc horrible vaut en fait 6.
Voilà :++:

6 est effectivement solution. Mais comment le trouves-tu ? Tu essayes successivement tous les entiers (positifs et négatifs) en partant de 0 ? Heureusement que la solution est 6 et non 9825...

[Zweig]

Une autre manière de faire.

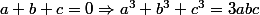
1) Montrer que pour tout triplet de réels (a,b,c) on a : (indice : regarde dans un de mes messages postés sur un de tes topics du forum Collège Lostounet, sur les équations, vers le mois d'Octobre-Novembre 2009)

2) En choisissant convenablement ces trois réels, montrer que la relation suivante se ramène à une équation du troisième degré. En déduire la seule solution réelle qui est 6.

[Zweig]

6 est effectivement solution. Mais comment le trouves-tu ? Tu essayes successivement tous les entiers (positifs et négatifs) en partant de 0 ? Heureusement que la solution est 6 et non 9825...

On peut coupler les règles des signes de Descartes avec le résultat suivant :

Soit un polynôme unitaire à coefficients entiers. Si est une racine entière de , alors

Dans notre cas,

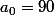
[Black Jack]

6 est effectivement solution. Mais comment le trouves-tu ? Tu essayes successivement tous les entiers (positifs et négatifs) en partant de 0 ? Heureusement que la solution est 6 et non 9825...

Toute équation du 3ème degré peut être résolue par la méthode de Cardan.

:zen:

[benekire2]

Je ne conaissais pas le résultat de Zweig, mais moi j'ai testé de 0 à 6 ...

tient d'ailleurs Zweig, t'aurais pas une preuve du fait que la racine entière divise le coef du monôme de plus haut degré ? Ca doit surement être bête...
Merci!

[Ben314]

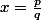
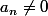
C'est effectivement trés simple : si (irréductible) est un quotient racine du polynôme à coeff. entiers (et évidement ) alors on a
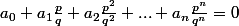
donc
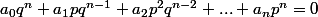
ce qui implique que :
et que
donc divise et divise .
Comme grâce au lemme de Gauss, cela implique que divise et divise .

Cela signifie que,
1) Pour trouver les racines rationelles d'un polynôme à coeff entier, il n'y a qu'un nombre fini de rationnels à tester (ceux tels que divise et divise )
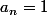
2) Si en fait est un polynôme unitaire () à coeff entiers, les éventuelles racines rationelle de , sont en fait entières.

[benekire2]

ok, merci bien :zen:

[ffpower]

Toute équation du 3ème degré peut être résolue par la méthode de Cardan.

:zen:

Sauf qu'on va tourner en rond

[Olympus]

Une autre manière de faire.

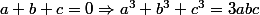
1) Montrer que pour tout triplet de réels (a,b,c) on a : (indice : regarde dans un de mes messages postés sur un de tes topics du forum Collège Lostounet, sur les équations, vers le mois d'Octobre-Novembre 2009)

Suffit de remarquer que ^^

[Lostounet]

Cette discussion est un peu sortie du cadre 'collège' vous ne trouvez pas? :ptdr:

[Black Jack]

Sauf qu'on va tourner en rond

Pourquoi tournerait-on en rond ?

Il a été montré que le résultat était une solution réelle de l'équation x³ - 21x - 90 = 0

On a donc une équation de la forme x³ - px + q = 0 avec (q/2)² + (p/3)³ = 45² - 7³ = 1682 > 0 et la méthode de Cardan arrive alors à :

Il y a donc une seule racine réelle R = ((-(q/2)+((q/2)² + (p/3)³)^(1/2))^(1/3)) + ((-(q/2) - ((q/2)² + (p/3)³)^(1/2))^(1/3)) et 2 racines complexes conjuguées qui ici ne nous intéressent pas.

R = ((-(q/2)+((q/2)² + (p/3)³)^(1/2))^(1/3)) + ((-(q/2) - ((q/2)² + (p/3)³)^(1/2))^(1/3))
R = ((-(-90/2)+((-90/2)² + (-21/3)³)^(1/2))^(1/3)) + ((-(-90/2) - ((-90/2)² + (-21/3)³)^(1/2))^(1/3))
R = 6.

:zen:

[ffpower]

R = ((-(-90/2)+((-90/2)² + (-21/3)³)^(1/2))^(1/3)) + ((-(-90/2) - ((-90/2)² + (-21/3)³)^(1/2))^(1/3))
R = 6. :zen:

Le passage de R=truc moche à R=6 est précisément la question initiale posée, donc si tu le justifies directement, ct bien la peine de faire le reste :happy2:

[Doraki]

6 est effectivement solution. Mais comment le trouves-tu ? Tu essayes successivement tous les entiers (positifs et négatifs) en partant de 0 ? Heureusement que la solution est 6 et non 9825...

On peut calculer une valeur approchée du truc avec une calculatrice.

Et même avec des approximations brutales des racines, on trouve que 1 < x < 8