Une seule question sur les vecteurs [3ème]

par **Mattcoure** » 14 Avr 2006, 16:12

:we: salut ! j'ai un tout petit probleme sur les vecteurs, mais pas moyen de trouver voir figure)

Placer 3 points ADC non aligné et construire le vecteur DB = vecteur DA + DC

La parallèle a ( AC) passant par B coupe (AD) en E et ( DC) en F

1)Démontrer que vecteur AC = vecteur EB et que vecteur AC = vecteur BF

MErci d avance

par **Touriste** » 14 Avr 2006, 20:08

Bonsoir,

Il y a beaucoup de droites parallèles dans ta figure : par exemple, (AB) et (CD) ainsi que (AC) et (BF). Tu peux en déduire la nature du quadrilatère ACFB et conclure pour l'une des égalités. Avec un raisonnement analogue, tu obtiens l'autre.
A+

par **Mattcoure** » 24 Avr 2006, 12:50

Merci ! Mais j'aimerais démontrer que AD = AE, mais je ne sais pas comment faire !

Merci d'avance ( en attente de :id: )

par **Zebulon** » 24 Avr 2006, 13:05

Bonjour,
si dans un quadrilatère les côtés opposés sont parallèles, alors c'est un parallélogramme et les côtés opposés sont égaux.
Zeb.

par **Mattcoure** » 25 Avr 2006, 10:17

Merci Zebulon :briques: ! Mais dans ma figure, ABDC est un parallélogramme. Pour démontrer que vecteur AC = vecteur EB, il me faudrait prouver que vecteur AD = vecteur EA ! Mais je ne sais pas comment faire.

Ainsi, en ayant prouvé que AD = EA, je pourrais prouver que AC = EB !

Merci d'avance :we:

par **Zebulon** » 25 Avr 2006, 10:32

Bonjour,
il n'y a pas besoin de montrer que

.
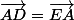
On a:

donc ABCD est un parallélogramme donc (AD) est parallèle à (BC) donc (AE) est parallèle à (BC) donc AEBC est un trapèze.
De plus, (AC) est parallèle à (EB) donc AEBC est un parallélogramme donc

.
Je te laisse montrer que

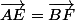
, c'est analogue à ma démonstration.
Bon courage.

par **Mattcoure** » 25 Avr 2006, 20:21

MErci Zebulon ! :id:

Une seule question sur les vecteurs [3ème]

Une seule question sur les vecteurs [3ème]

Qui est en ligne