Triangles rectangles et equations
Réponses à toutes vos questions du CP à la 3ème
-
TIDOU
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Jan 2009, 16:26
-
 par TIDOU » 12 Jan 2009, 20:15
par TIDOU » 12 Jan 2009, 20:15
c'est z+1 qui est la valeur de L'hypoténuse
-
TIDOU
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Jan 2009, 16:26
-
 par TIDOU » 12 Jan 2009, 20:19
par TIDOU » 12 Jan 2009, 20:19
Quelle est l'equation facile à résoudre dans le e) alors ?
-
mathelot
 par mathelot » 12 Jan 2009, 20:25
par mathelot » 12 Jan 2009, 20:25
TIDOU a écrit:c'est z+1 qui est la valeur de L'hypoténuse
ok. exact.
profites-en pour réécrire l'égalité de Pythagore.
-
TIDOU
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Jan 2009, 16:26
-
 par TIDOU » 12 Jan 2009, 21:10
par TIDOU » 12 Jan 2009, 21:10
(Z+1)²=z²+(z-1)² ?
-
mathelot
 par mathelot » 12 Jan 2009, 21:18
par mathelot » 12 Jan 2009, 21:18
TIDOU a écrit:(Z+1)²=z²+(z-1)² ?
oui, très bien. ne confonds pas Z majuscule et z minuscule.
maintenant, il suffit de développer les deux identités remarquables:
^2)
et
^2)
sais tu faire ? sinon google "identités remarquables"
-
TIDOU
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Jan 2009, 16:26
-
 par TIDOU » 12 Jan 2009, 21:28
par TIDOU » 12 Jan 2009, 21:28
OUI, ça je sais mais comment dire que c'est celle la plus facile à résoudre si tel est le cas ? puisque j'ai réussi a faire toutes les autres équations et que je n'ai pas eu de problème ?
-
mathelot
 par mathelot » 12 Jan 2009, 22:26
par mathelot » 12 Jan 2009, 22:26
TIDOU a écrit:(Z+1)²=z²+(z-1)² ?
ok, je termine:
1ère égalité de Pythagore
^2=(x+1)^2+x^2)
donne

est-ce que l'on sait résoudre ce genre d'équation ? non.
2ème égalité de Pythagore
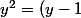^2+(y-2)^2)
donne

3ème égalité de Pythagore
^2=z^2+(z-1)^2)
donne
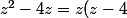=0)
équation produit, facile à résoudre.
-
TIDOU
- Membre Naturel
- Messages: 13
- Enregistré le: 11 Jan 2009, 16:26
-
 par TIDOU » 12 Jan 2009, 23:18
par TIDOU » 12 Jan 2009, 23:18
Merci Mathelot pour ton aide. Pour info j ai réussi a faire seul les autres exos de mon devoir. :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
