Triangles rectangles et equations
28 messages
- Page 1 sur 2 - 1, 2
Triangles rectangles et equations
Bonjour,
J'ai à résoudre ceci et je n'y arrive pas (j'y suis depuis ce matin...):
On cherche tous le traingles rectangles dont les longueurs des côtés sont 3 entiers consécutifs.
pour cela, repondre aux questions dui suivent.
a quel côté du triangle à pous longueur le plus grand de ces 3 nombres ?
b On note X la longueur du plus petit côté le l'angle droit. Nontrer que l'équation traduisant le problème est : x²-2x-3=0
c On note y la longueur de l'hipoténuse. Monter que l'équation obtenue est y²-6y+5=0
d On note z la longeur du côté de l'angle droit le plus long. Montrer que l'équation obtenue est z²-4z=0
e Parmi les 3 chix d'inconnues envisagées aux questions b,c,d quel est celui qui conduit à une équation facile à résoudre?
Résoudre cette équation et conclure.
J'ai à résoudre ceci et je n'y arrive pas (j'y suis depuis ce matin...):
On cherche tous le traingles rectangles dont les longueurs des côtés sont 3 entiers consécutifs.
pour cela, repondre aux questions dui suivent.
a quel côté du triangle à pous longueur le plus grand de ces 3 nombres ?
b On note X la longueur du plus petit côté le l'angle droit. Nontrer que l'équation traduisant le problème est : x²-2x-3=0
c On note y la longueur de l'hipoténuse. Monter que l'équation obtenue est y²-6y+5=0
d On note z la longeur du côté de l'angle droit le plus long. Montrer que l'équation obtenue est z²-4z=0
e Parmi les 3 chix d'inconnues envisagées aux questions b,c,d quel est celui qui conduit à une équation facile à résoudre?
Résoudre cette équation et conclure.
bonsoir,
b On note X la longueur du plus petit côté le l'angle droit. Nontrer que l'équation traduisant le problème est : x²-2x-3=0
x le plus petit côté, x+1 le moyen et x+2 l'hypoténuse
écris pythagore
c On note y la longueur de l'hipoténuse. Monter que l'équation obtenue est y²-6y+5=0
y l'hypoténuse
y-1 le moyen côté et y-2 le plus petit
pythagore
b On note X la longueur du plus petit côté le l'angle droit. Nontrer que l'équation traduisant le problème est : x²-2x-3=0
x le plus petit côté, x+1 le moyen et x+2 l'hypoténuse
écris pythagore
c On note y la longueur de l'hipoténuse. Monter que l'équation obtenue est y²-6y+5=0
y l'hypoténuse
y-1 le moyen côté et y-2 le plus petit
pythagore
re-aloha,
en algèbre, les nombres inconnus sont désignés par des lettres.
On essaye de transposer aux lettres le maximum d'opérations que l'on
sait faire sur des nombres.
Il y a des nombres très connus qui ont un nom ... très connu
le coeff de proportionnalité entre le périmètre d'un cercle et le diamètre
s'appelle
Le nombre d'or s'appelle
D'autres nombres ont une existence (une appelation ) éphémère.
ainsi , dans ton exercice, désigne le plus petit côté
désigne le plus petit côté
le coté moyen vaudra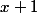
l'hypoténuse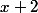
la longueur de l'hypoténuse sera nommé
Deux appelations peuvent désigner le même objet.
ainsi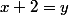
en algèbre, les nombres inconnus sont désignés par des lettres.
On essaye de transposer aux lettres le maximum d'opérations que l'on
sait faire sur des nombres.
Il y a des nombres très connus qui ont un nom ... très connu
le coeff de proportionnalité entre le périmètre d'un cercle et le diamètre
s'appelle
Le nombre d'or s'appelle
D'autres nombres ont une existence (une appelation ) éphémère.
ainsi , dans ton exercice,
le coté moyen vaudra
l'hypoténuse
la longueur de l'hypoténuse sera nommé
Deux appelations peuvent désigner le même objet.
ainsi
TIDOU a écrit:Bonsoir,
z est le noyen côté, on donne alors z-1 pour le petit côté et z+1 pour l'hypothenuse ?
oui, bravo, tout à fait. félicitations.
TIDOU a écrit: comment montrer les equations obtenues alors ?
Les autres équations se montrent de la même manière, grâce
au théorème de Pythagore.
Y en a que l'on sait factoriser et d'autres pas.
re Tidou,
Le triangle a trois côtés.
Chaque longueur de côté a un nom.
 = longueur du petit côté
= longueur du petit côté
 =longueur du côté intermédiaire
=longueur du côté intermédiaire
 = longueur de l'hypoténuse (le grand côté)
= longueur de l'hypoténuse (le grand côté)
Les longueurs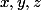 sont les inconnues d'équations
sont les inconnues d'équations
qui ne se ressemblent pas.
Il y a une seule équation qui est facile à résoudre. Pas les autres.
Le triangle a trois côtés.
Chaque longueur de côté a un nom.
Les longueurs
qui ne se ressemblent pas.
Il y a une seule équation qui est facile à résoudre. Pas les autres.
equation?
ca fait 2h que je suis dessus :
"on donne la série de données de nombres rangés dans l'odre croissants x;4;5;9;y
determiner la valeur de xet y sachant que la moyenne de cette série est 8 et que son étendue est 17"
merci d'avance
"on donne la série de données de nombres rangés dans l'odre croissants x;4;5;9;y
determiner la valeur de xet y sachant que la moyenne de cette série est 8 et que son étendue est 17"
merci d'avance
pol--iin a écrit:ca fait 2h que je suis dessus :
"on donne la série de données de nombres rangés dans l'odre croissants x;4;5;9;y
determiner la valeur de xet y sachant que la moyenne de cette série est 8 et que son étendue est 17"
merci d'avance
pourquoi ne crées-tu pas ton propre post au lieu de squatter!!!
sinon :
étendue=différence entre la valeur la plus haute (ici y) et la valeur la plus basse de la variable (ici x)=17
moyenne=(somme des variables)/nombre de variables=8
tu obtiens 2 équations à 2 inconnues
résous le système pour trouver x et y
28 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
