Titre non conforme - Attention
Réponses à toutes vos questions du CP à la 3ème
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 18 Jan 2009, 15:47
par Timothé Lefebvre » 18 Jan 2009, 15:47
Pourquoi tu multiplies tout ?
n+n+1+n+2 = 78
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 18 Jan 2009, 15:47
par Clembou » 18 Jan 2009, 15:47
Mais sinon tu peux simplifier ton equation en considérant l'entier
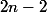
,

et
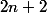
...
-
nsa
- Membre Relatif
- Messages: 123
- Enregistré le: 18 Jan 2009, 13:58
-
 par nsa » 18 Jan 2009, 15:51
par nsa » 18 Jan 2009, 15:51
je multiplie pour montrer que "n" est un nombre pair vue que la consigne est :
la somme de trois entiers pairs consécutifs est 78
calculer ces nombres
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 18 Jan 2009, 15:53
par Clembou » 18 Jan 2009, 15:53
Ok ! Et tu as lu mon indication ?
-
nsa
- Membre Relatif
- Messages: 123
- Enregistré le: 18 Jan 2009, 13:58
-
 par nsa » 18 Jan 2009, 15:55
par nsa » 18 Jan 2009, 15:55
oui
donc (2n-2)+2n+(2n+2)
(2x13-2)+2x13+(2x13+2)
ça suffit pour calculer les nombres?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 18 Jan 2009, 16:01
par Clembou » 18 Jan 2009, 16:01
Ba non... Pourquoi 13 tout de suite ??
Non, faut que tu résoud simplement :
+(2n)+(2n+2) = 78)
-
nsa
- Membre Relatif
- Messages: 123
- Enregistré le: 18 Jan 2009, 13:58
-
 par nsa » 18 Jan 2009, 16:06
par nsa » 18 Jan 2009, 16:06
ah ok
(2n-2)+2n+(2n+2) = 78
6n=78
n=78/6
n=13
ensuite je fais
(26-2)+26+(26+2)=78
24+26+28=78
et après je conclue c'est ça?
merci d'avoir conssacré une partie de votre temps pour m'aidé
bonne fin de journée et bonne continuation
à la prochaine
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 18 Jan 2009, 16:08
par Clembou » 18 Jan 2009, 16:08
nsa a écrit:ah ok
(2n-2)+2n+(2n+2) = 78
6n=78
n=78/6
n=13
ensuite je fais
(26-2)+26+(26+2)=78
24+26+28=78
et après je conclue c'est ça?
merci d'avoir conssacré une partie de votre temps pour m'aidé
bonne fin de journée et bonne continuation
à la prochaine
Tu conclus que 24,26,28 sont les nombres que tu cherches. Ok, ça marche :++:
A bientôt sur le forum :++:
-
nsa
- Membre Relatif
- Messages: 123
- Enregistré le: 18 Jan 2009, 13:58
-
 par nsa » 18 Jan 2009, 19:12
par nsa » 18 Jan 2009, 19:12
Bonsoir
j'ai encore un problème avec ce DM
je n'arrive pas a résoudre cette équation:
2x+1 - x-3 = x+2 +2
----- ----- -----
2 ....... 10 ..... 5
ps : les pointillés représente la barre de fraction
ps2 : les petits points ne représentent rien
ps3 : bah j'espère l'avoir ^^
merci d'avance
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 18 Jan 2009, 19:41
par Clembou » 18 Jan 2009, 19:41
nsa a écrit:Bonsoir
j'ai encore un problème avec ce DM
je n'arrive pas a résoudre cette équation:
2x+1 - x-3 = x+2 +2
----- ----- -----
2 ....... 10 ..... 5
ps : les pointillés représente la barre de fraction
ps2 : les petits points ne représentent rien
ps3 : bah j'espère l'avoir ^^
merci d'avance
A te revoilà :++:
Je n'ai pas trop compris l'équation... Utilises les balises tex pour les fractions \frac{numérateur}{dénominateur}.
Merci

-
nsa
- Membre Relatif
- Messages: 123
- Enregistré le: 18 Jan 2009, 13:58
-
 par nsa » 18 Jan 2009, 20:22
par nsa » 18 Jan 2009, 20:22

-

=

+2
voilà la fraction et merci pour l'aide
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 18 Jan 2009, 20:23
par Clembou » 18 Jan 2009, 20:23
Up :++: Tu peux me traduire ton énoncé avec les balises TeX avec ce que je t'ai indiqué en MP. Merci :we:
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 18 Jan 2009, 20:24
par Clembou » 18 Jan 2009, 20:24
Là, il faut mettre au même dénominateur. Essaie d'avoir un dénominateur commun égal à 10...
-
nsa
- Membre Relatif
- Messages: 123
- Enregistré le: 18 Jan 2009, 13:58
-
 par nsa » 18 Jan 2009, 20:28
par nsa » 18 Jan 2009, 20:28
les termes de droite aussi?
avec 10 en dénominateur?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 18 Jan 2009, 20:32
par Clembou » 18 Jan 2009, 20:32
Oui voilà ! :++: Qu'est ce que ça donne ?
-
nsa
- Membre Relatif
- Messages: 123
- Enregistré le: 18 Jan 2009, 13:58
-
 par nsa » 18 Jan 2009, 20:43
par nsa » 18 Jan 2009, 20:43

=

la je bloque
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 18 Jan 2009, 20:44
par Clembou » 18 Jan 2009, 20:44
Multiplies par 10 des deux côtés de l'équation pour éliminer les dénominateurs :++: et ensuire, résolution d'une équation simple
-
nsa
- Membre Relatif
- Messages: 123
- Enregistré le: 18 Jan 2009, 13:58
-
 par nsa » 18 Jan 2009, 20:46
par nsa » 18 Jan 2009, 20:46
comme résultat je trouve
x=

c'est ça?
-
Clembou
- Membre Complexe
- Messages: 2732
- Enregistré le: 03 Aoû 2006, 11:00
-
 par Clembou » 18 Jan 2009, 20:49
par Clembou » 18 Jan 2009, 20:49
Heu non ! Est-ce que tu peux développer les étapes de calcul stp :++:
-
nsa
- Membre Relatif
- Messages: 123
- Enregistré le: 18 Jan 2009, 13:58
-
 par nsa » 18 Jan 2009, 20:55
par nsa » 18 Jan 2009, 20:55

=

je multiplie par 10
9x+2=2x+24
9x-2x=24-2
7x=22
x=

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
