Sinus/cosinus/tangente Aie Aie !!!!

[lenalena]

re bonjour,

En premier lieu merci à ceux qui m'aide pour mon dm de rentrée parce que c'est pas évident de faire huit exercices quand on est pas trop doué.
J'au un nouveau problème que j'arrive pas trop à faire.

Soit deux bateaux au large d'une ile de forme triangle rectangle en C.

AB sont séparés de 800 mètres et ce segment est l'hypoténuse, on ne connait pas la valeur de AC qui est le côté adjacent de CAB et le côté BC dont on ne connait pas la longueur est donc l'opposé de CAB.
On sait que l'angle aigu A est de 35° et l'angle de B est de 55°. On me dit que les bâteaux ne voient pas l'île en C sous le même angle et on me demande de déterminer au mètre près, la dista,nce qui sépara chaque bateau de l'ile.

Je ne sais pas du tout comment aborder ce problème ! pourriez vous m'aider et me guider ? merci bcp à vous.

[lenalena]

re bonjour,

En premier lieu merci à ceux qui m'aide pour mon dm de rentrée parce que c'est pas évident de faire huit exercices quand on est pas trop doué.
J'au un nouveau problème que j'arrive pas trop à faire.

Soit deux bateaux au large d'une ile de forme triangle rectangle en C.

AB sont séparés de 800 mètres et ce segment est l'hypoténuse, on ne connait pas la valeur de AC qui est le côté adjacent de CAB et le côté BC dont on ne connait pas la longueur est donc l'opposé de CAB.
On sait que l'angle aigu A est de 35° et l'angle de B est de 55°. On me dit que les bâteaux ne voient pas l'île en C sous le même angle et on me demande de déterminer au mètre près, la dista,nce qui sépara chaque bateau de l'ile.

Je ne sais pas du tout comment aborder ce problème ! pourriez vous m'aider et me guider ? merci bcp à vous.

N'aynt pas eût de réponse je me suis lancée dans mon problème mais si quelqu'un peut me dire si c'est bon je vous remercie.

Alors on a l'hypothénuse de IAB = 800 mètres et je veux connaître la longueur de BI (côté oppose à I). J'ai donc appliqué un sinus : sinus 55°(degré de l'angle b) = 800 m x sin 55° = 655,32mètres

et j'ai calculé l'autre longueur manquante soir AI côté adjaçent en utilisant un cosinus : cos 35° (angle de A) = 800xcos 35° et là je tombe aussi sur 655,32 mètre.

Ce qui veut dire que les deux bateaux seraint à la même distance de l'ile point I ?

Je sais c'est laborieux mais merci de votre correction.

[Frednight]

Pas d'accord : il faut utiliser le cosinus dans les deux cas.

Pour retenir les conditions d'application en général, une phrase à retenir :
SOH-CAH-TOA
qui se traduit par :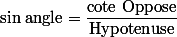 , 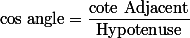et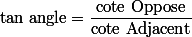

Pour l'angle dont tu connais la valeur, les côtés qui t'intéressent sont l'hypoténuse AB que tu connais également et le côté AC dont tu cherches la longueur, qui est en fait le côté adjacent à ton angle.
En regardant dans les formules citées ci-dessus, tu vois bien que la seule équation regroupant ces trois paramètres est celle faisant intervenir le cosinus.


P.S. : je pense que l'énoncé est mal formulé : ce n'est pas l'île qui est de forme triangulaire. C est à mon sens le point représentant l'île par rapport aux points A et B qui représentent les bateaux, ces trois points formant un triangle rectangle en C.

[LeJeu]

N'aynt pas eût de réponse je me suis lancée dans mon problème mais si quelqu'un peut me dire si c'est bon je vous remercie.

Alors on a l'hypothénuse de IAB = 800 mètres et je veux connaître la longueur de BI (côté oppose à I). J'ai donc appliqué un sinus : sinus 55°(degré de l'angle b) = 800 m x sin 55° = 655,32mètres

et j'ai calculé l'autre longueur manquante soir AI côté adjaçent en utilisant un cosinus : cos 35° (angle de A) = 800xcos 35° et là je tombe aussi sur 655,32 mètre.

Ce qui veut dire que les deux bateaux seraint à la même distance de l'ile point I ?

Je sais c'est laborieux mais merci de votre correction.

Regarde de plus , mais tu as calculé deux fois la longueur du même coté .... ( une fois comme coté opposé d'un angle, une fois comme coté adjacent de l'angle opposé ...)

la longueur qui te manque se trouve avec le sin 35° !

[lenalena]

Regarde de plus , mais tu as calculé deux fois la longueur du même coté .... ( une fois comme coté opposé d'un angle, une fois comme coté adjacent de l'angle opposé ...)

la longueur qui te manque se trouve avec le sin 35° !

Merci de votre aide!!. Alors si j'ai bien compris je dois reprendre le cosinus de 55° (angle BC) et le sinus de 35° (angle AC) et là oui on arrive pas aux mêmes distance : BC est à 655,32mètres et AC serait à 458,86 mètres. A moins que ce soit BC 458 et AC 655 car en regardant le dessin je me dis qu'à l'échelle A me semble plus loin que BC.

Mais ce que je ne comprends pas c'est pourquoi je dois appliquer deux cosinus alors que je recherche 1/ la longueur du côté opposé B/ la longueur du côté adjacent à AB :mur: Je voudrais pas paraître bête mais là quelque chose m'échappe... ? pourriez vous m'éclaircir ? merci beaucoup de votre patience

[Frednight]

selon moi il faut que tu utilises deux fois le cosinus.
Ensuite fais attention : lorsque l'on parle de côté adjacent ou opposé c'est par rapport à l'angle entre ces deux côtés

[LeJeu]

Mais ce que je ne comprends pas c'est pourquoi je dois appliquer deux cosinus alors que je recherche 1/ la longueur du côté opposé B/ la longueur du côté adjacent à AB :mur: Je voudrais pas paraître bête mais là quelque chose m'échappe... ? pourriez vous m'éclaircir ? merci beaucoup de votre patience

je complète ce que dis Fred :

Si tu considères l'angle A,
tu calcules AC avec le cosinus de l'angle en A ( coté adjacent)
tu calcules BC avec le sinus de l'angle en A ( coté opposé)

s' il te prend l'idée de changer l'angle pour le calcul du deuxième coté
tu calcules BC avec le cos de l'angle en B( coté adjacent)

Et oui ! le sin de l'angle A = le cos de l'angle B ...

[lenalena]

je complète ce que dis Fred :

Si tu considères l'angle A,
tu calcules AC avec le cosinus de l'angle en A ( coté adjacent)
tu calcules BC avec le sinus de l'angle en A ( coté opposé)

s' il te prend l'idée de changer l'angle pour le calcul du deuxième coté
tu calcules BC avec le cos de l'angle en B( coté adjacent)

Et oui ! le sin de l'angle A = le cos de l'angle B ...

merci beaucoup pur toutes ces explications je les revoient demain ! bonne soirée et encore merci